文/小只
方差分析在市场及用户研究领域中,用于比较多个群体之间的均值差异。同时帮助研究者理解不同变量对某一结果的影响,还能揭示多个因素的交互效应。
核心思想是通过比较组内方差与组间方差,来判断不同组别之间是否存在显著差异。
简单来说,方差分析能告诉我们,多个群体的平均水平是否一致,或者这些群体的差异是否足以说明某种潜在规律。
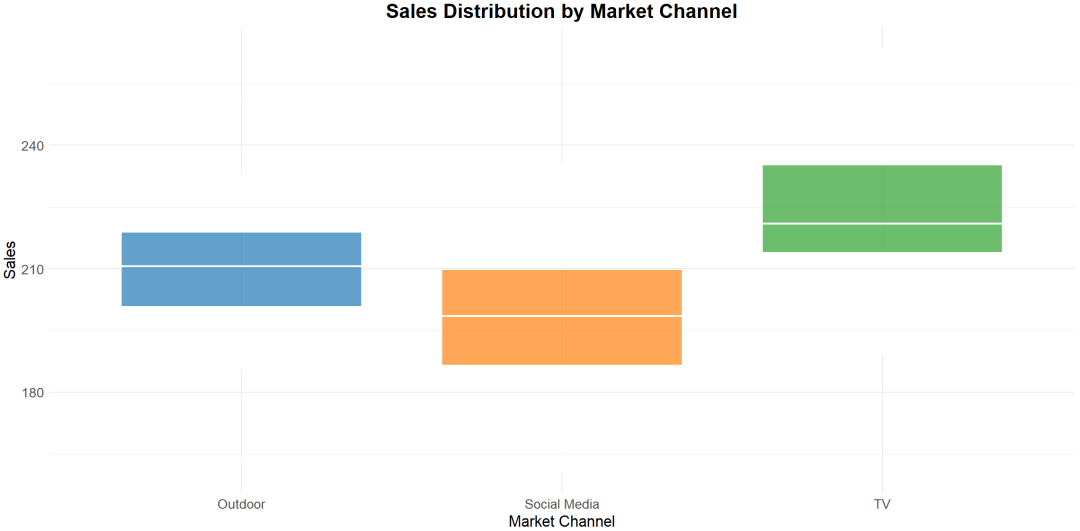
在方差分析中,我们将总变异分为两部分:组内变异和组间变异。
组内变异反映的是每个组内的个体差异,而组间变异则反映了不同组之间的差异。
通过计算组间方差与组内方差的比值(即F值),我们可以判断这种差异是否具有统计显著性。
① 正态性假设
定义:正态性假设要求每个组的数据应该来自正态分布的总体。这意味着所有组的因变量应该在各自的组内近似服从正态分布。
处理方法:如果数据不服从正态分布,可能需要进行数据变换(如对数变换)或使用非参数检验方法来替代。
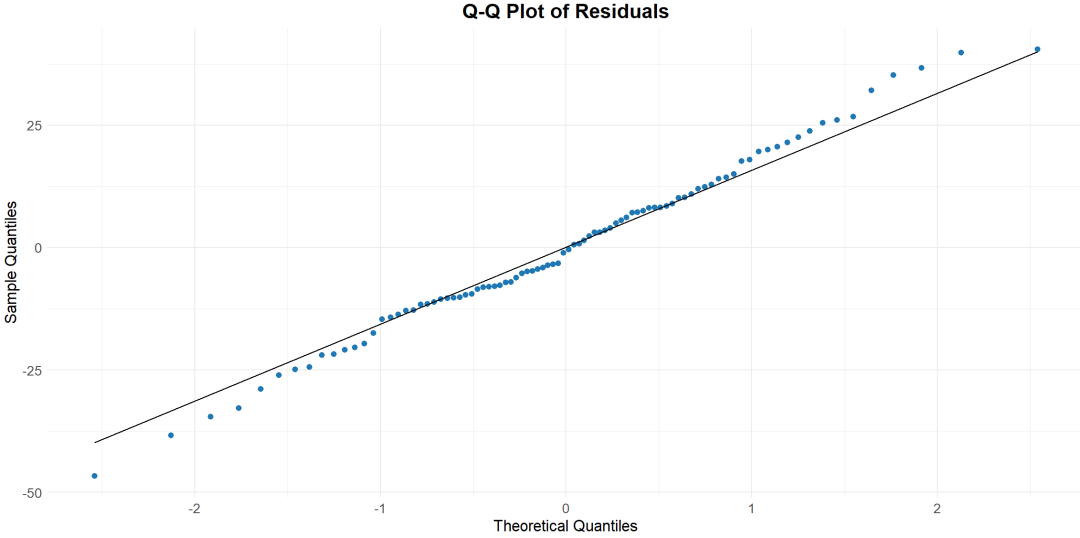
② 方差齐性假设
定义:方差齐性假设要求各组数据的方差应当相等或近似相等。
处理方法:
如果数据的方差不齐,可考虑以下方法:
数据变换 or 使用Welch方差分析 or 采用非参数检验。
③ 独立性假设
定义:独立性假设要求数据样本之间是相互独立的,每个被试或样本都是随机选取的。
④ 因变量的连续性
定义:方差分析通常假设因变量是连续的,即因变量可以在某个范围内取任意数值。
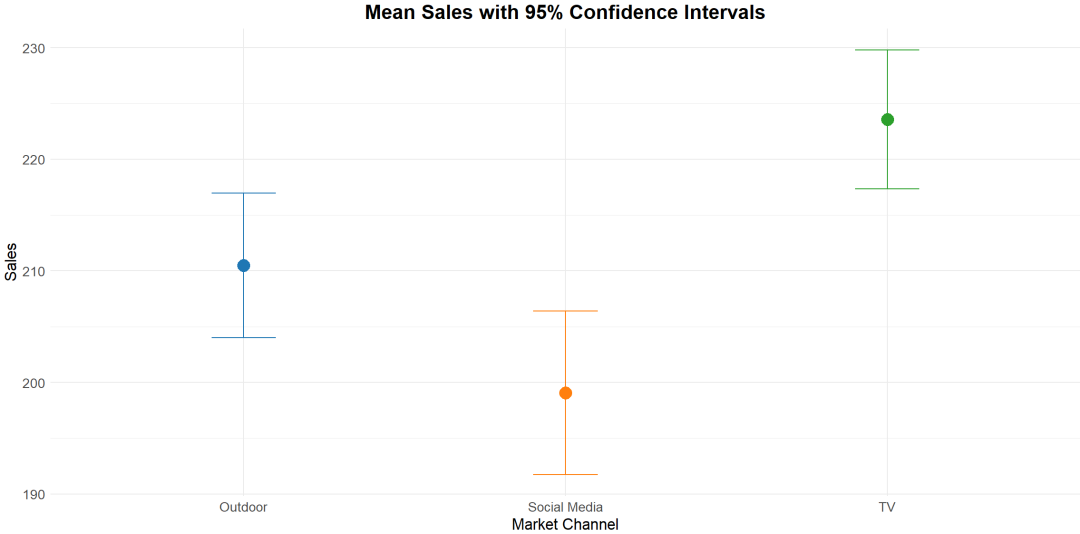
步骤1:制定假设
首先需要制定零假设(H0)和备择假设(H1)。
零假设通常表示各组别之间没有显著差异,而备择假设则表示至少有一组之间存在差异。
例如,在广告策略的研究中,零假设可以是“广告策略A、B、C对购买意向的影响没有差异”。
步骤2:计算F值
F值是方差分析的核心统计量,用于判断不同组别之间的差异是否显著。
计算F值的过程涉及到计算组内和组间的均方(即方差的估计值),然后将组间均方除以组内均方。
步骤3:查表判断显著性
在计算出F值后,我们需要将其与统计表中的临界值进行比较。
如果计算得到的F值大于表中的临界值,则拒绝零假设,认为组别间存在显著差异。
步骤4:结果解释
如果方差分析的结果表明存在显著差异,接下来可进行事后检验(如Tukey HSD检验)来确定具体哪些组之间存在差异。
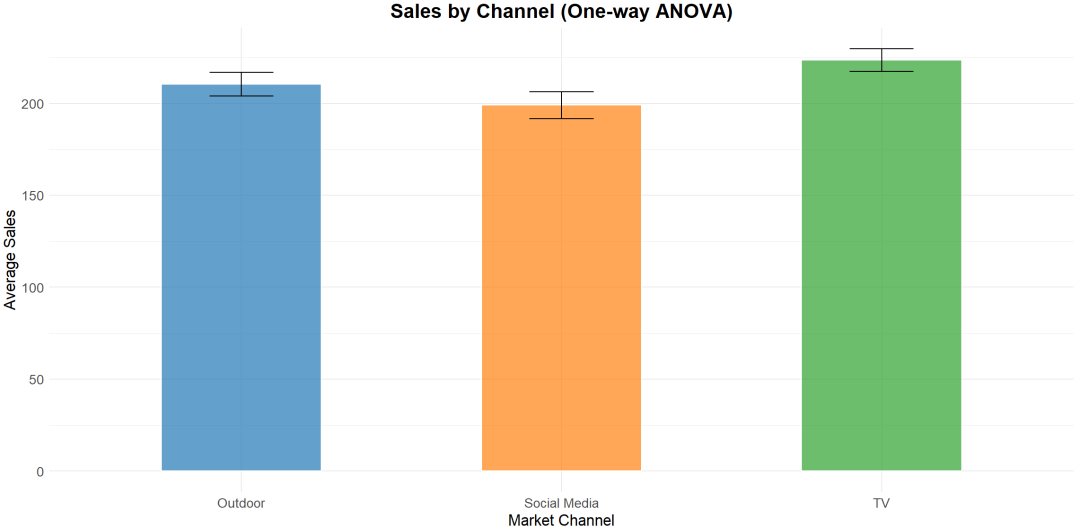
单因素方差分析(One-way ANOVA)
理解 : 用于比较 三个或更多独立组的均值差异 ,这些组之间 只有一个自变量(因素) 进行区分。
当你有多个组数据,想知道它们的平均值是否存在差异,而这个差异只由一个因素决定,适用单因素方差分析。
适用前提条件:
① 各组样本来自正态分布的总体。
② 各组样本具有相同的方差。
③ 自变量为分类变量,且可包含多个类别。
自变量类型:分类变量(多个类别)
因变量类型:连续变量
示例:常用于市场细分研究中,如比较不同市场细分群体对产品的反应。
理解 : 分析 多个自变量 (因素)对 单个因变量 的影响。
①用于比较多个组的均值差异;
②确定哪种因素或因素组合对结果有显著影响;
③这些因素之间有何交互作用。
适用前提条件:
① 所有组的因变量应该来自正态分布的总体。
② 各组的因变量方差应该相等。
③ 各组样本应相互独立。
自变量类型:分类变量(名义或有序类别)。
因变量类型:连续变量,通常是间隔或比例数据。
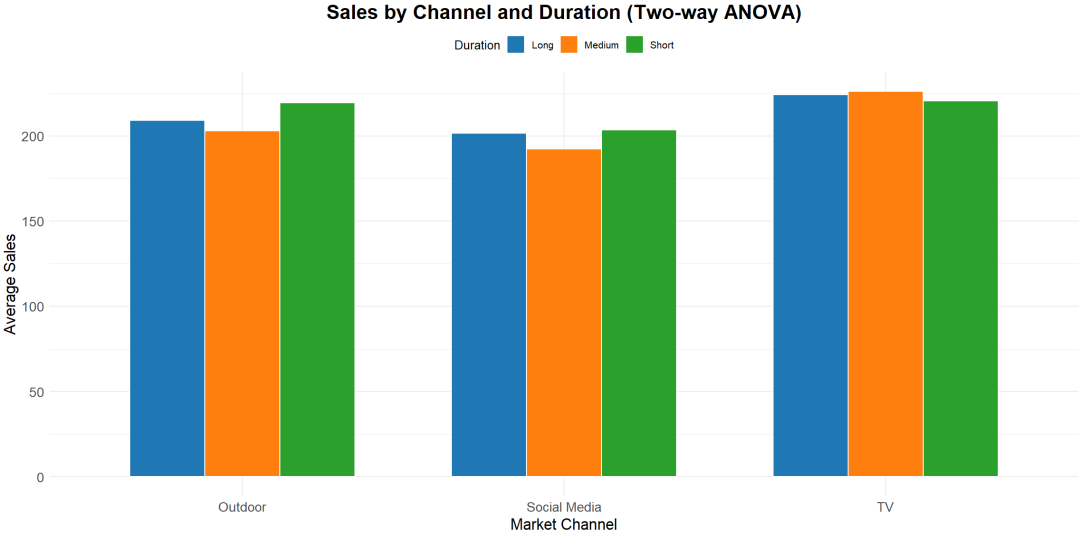
示例:如评估不同市场策略(如促销方式和广告渠道)对销售表现的影响。
理解:分析一个或多个自变量对多个因变量的影响。
当你有多个相关的因变量,并希望同时研究它们如何受到自变量的影响时。
适用前提条件:
① 每个组内多个因变量的联合分布应服从多元正态分布。
② 所有组的因变量方差-协方差矩阵应相等。
③ 因变量之间应存在一定的相关性,若因变量独立,使用多个单变量方差分析(ANOVA)更为适宜。
自变量类型:分类变量,可以包含多个类别。
因变量类型:多个连续变量。
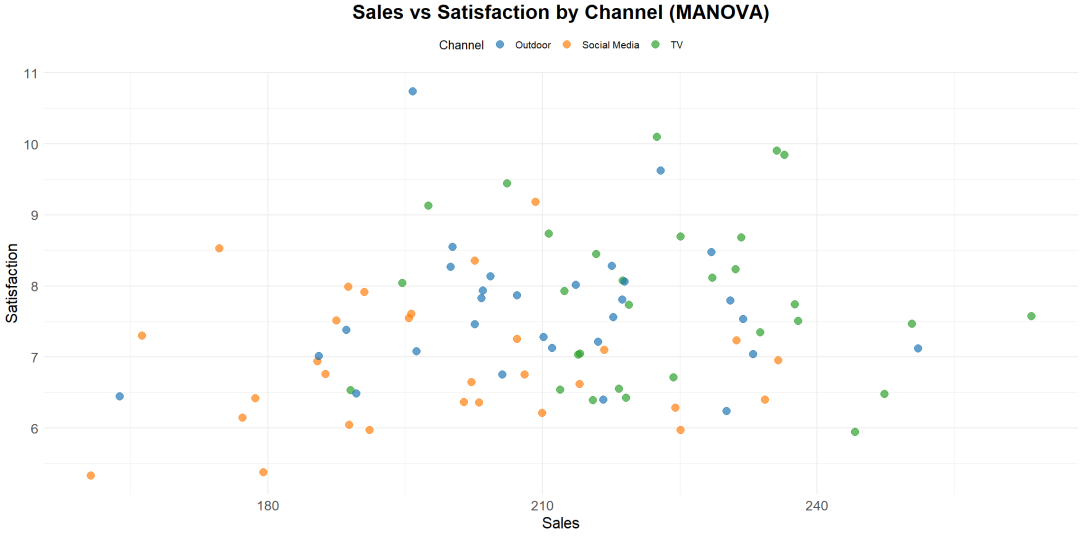
示例:如果你想研究不同广告策略(如电视广告、社交媒体广告和线下促销活动)对多个用户反应指标的联合影响,你可以使用MANOVA来同时分析这些广告策略对满意度、品牌认知度和购买意愿的影响。
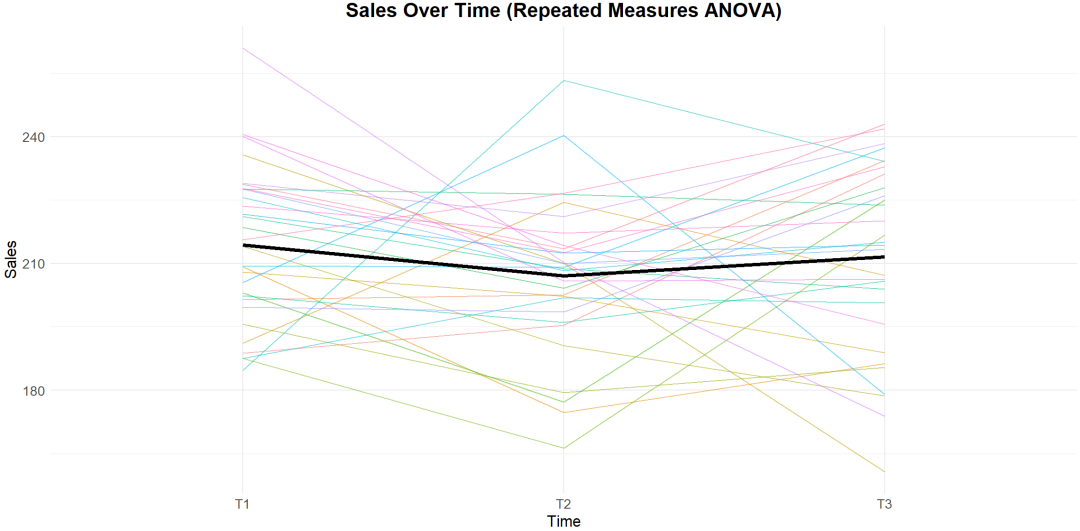
重复测量方差分析(Repeated Measures ANOVA)
理解:用于比较同一组样本在不同时间点或条件下的均值差异,通常用于纵向研究。
当你对同一组样本在多个时间点进行了测量,想知道这些测量值是否显著不同,适用重复测量方差分析。
适用前提条件:
① 数据是相关的(同一组样本)。
② 样本来自正态分布的总体。
自变量类型:分类变量(时间或条件)
因变量类型:连续变量
示例:适用于纵向研究和时间序列分析,如评估用户随着时间对产品满意度的变化。
理解:同时比较多个组之间的均值差异(被试间因素)和同一组内不同条件下的均值差异(被试内因素)。
适用前提条件:
① 各组样本数据应来自正态分布的总体。
② 对于被试间因素,各组数据应具有相同的方差。
③ 对于被试内因素,数据应满足球形假设,即相邻测量之间的差异应具有相同的方差。
自变量类型:包含一个或多个被试间分类变量(组间因素)和一个或多个被试内分类变量(组内因素)。
因变量类型:连续变量。
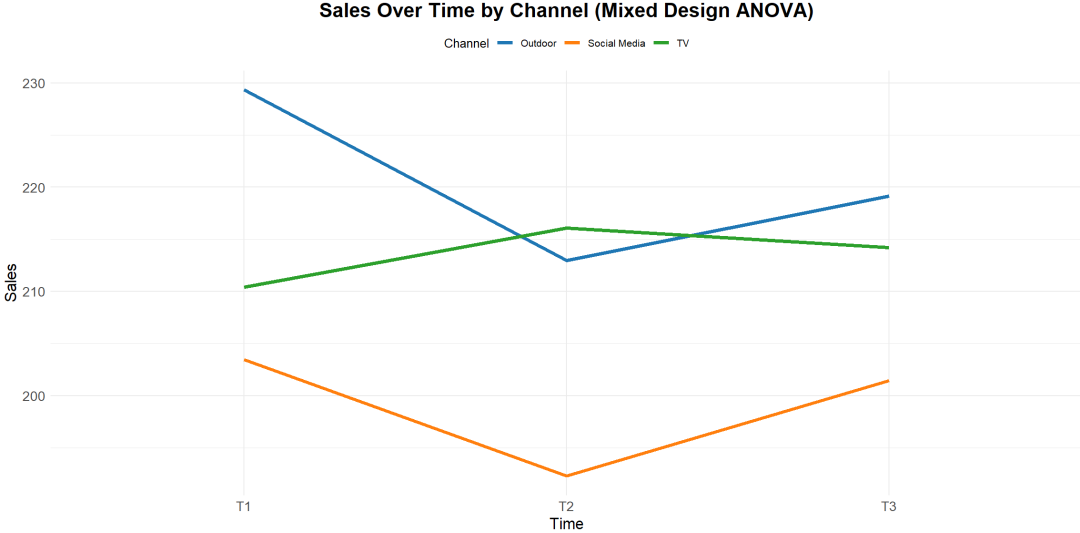
示例:假设你想研究三种不同的广告文案在不同的市场细分群体(如年龄段、性别或地域)中的效果,同时又想观察同一群体在不同时间点对广告的反应变化。混合设计方差分析可以帮助分析广告文案和用户群体的交互作用,以及时间因素对用户反应的影响。
理解:对MANOVA的扩展,适用于分析多个因变量,同时控制一个或多个协变量的影响。
协变量(Covariate)是指那些可能影响因变量,但在研究中并不是主要关注的变量。协变量通常是连续型变量,通常与因变量有一定的相关性,而MANCOVA能够帮助消除协变量对因变量的影响,从而更加准确地评估自变量对因变量的作用。
适用前提条件:
① 每个组内多个因变量的联合分布应服从多元正态分布。
② 所有组的因变量方差-协方差矩阵应相等。
③ 协变量与因变量之间应存在线性关系。
④ 因变量之间应存在一定的相关性。
自变量类型:分类变量,可以包含多个类别。
因变量类型:多个连续变量。
协变量类型:连续变量为主。
示例:
可以研究不同促销策略(如限时折扣、会员积分)对用户购买行为和忠诚度的影响,同时控制用户的购买历史;或者分析不同品牌广告对用户品牌态度和购买意向的影响,同时控制用户对品牌的初始认知水平。
通过MANCOVA,可以更准确地分析自变量对多个因变量的独立影响,排除协变量的干扰。
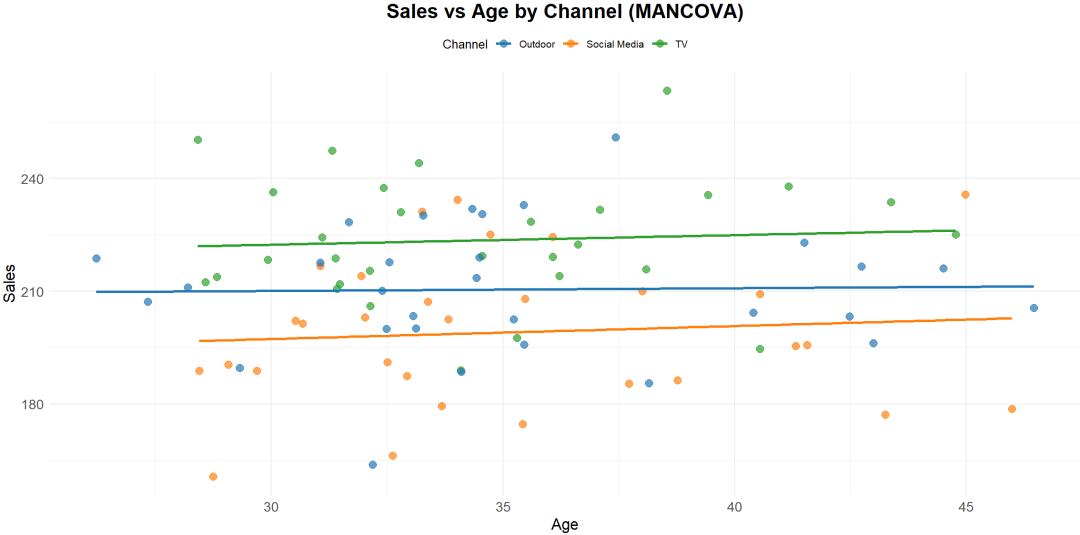
以"广告策略对购买意向的影响"为例
背景介绍
假设我们是一家市场研究公司,受托研究某公司三种不同广告策略(电视广告、社交媒体广告、邮件营销)对消费者购买意向的影响。我们随机选择了150位消费者,并将他们分成三组,每组50人,分别暴露在不同的广告策略下。我们的研究目标是比较这三种广告策略是否对购买意向有显著影响。
步骤1:数据收集与整理
首先,我们收集了每个消费者在接触广告后的购买意向评分(1-10分)。然后,我们将数据整理成表格,分为三列,每列对应一种广告策略。
步骤2:方差分析计算
我们使用Excel或统计软件(如SPSS、R)进行单因素方差分析。
计算过程包括计算每组的均值、组内方差、组间方差以及最终的F值。
步骤3:结果解释
假设方差分析结果显示F值为5.67,而临界值为3.09(根据自由度查表)。因为F值大于临界值,我们拒绝零假设,认为不同广告策略对购买意向的影响存在显著差异。
步骤4:事后检验
接下来,我们进行事后检验以确定具体哪些广告策略之间存在差异。
假设结果显示电视广告和社交媒体广告之间的差异显著,而社交媒体广告和邮件营销之间没有显著差异。
① 假设条件的限制
方差分析基于一定的统计假设,如正态分布、方差齐性(各组方差相等)等。
如果这些假设不成立,分析结果可能会受到影响。
② 方差分析与因果关系
需要注意的是,方差分析只能揭示组间的均值差异,但并不能直接推断因果关系。
市场研究者在解释方差分析结果时,应谨慎对待因果推论,避免过度解释。
③ 多重检验问题
当同时进行多个方差分析时,可能会增加误报(即I类错误)的概率。
研究者应考虑多重检验校正方法,如Bonferroni校正,以降低错误发现的风险。
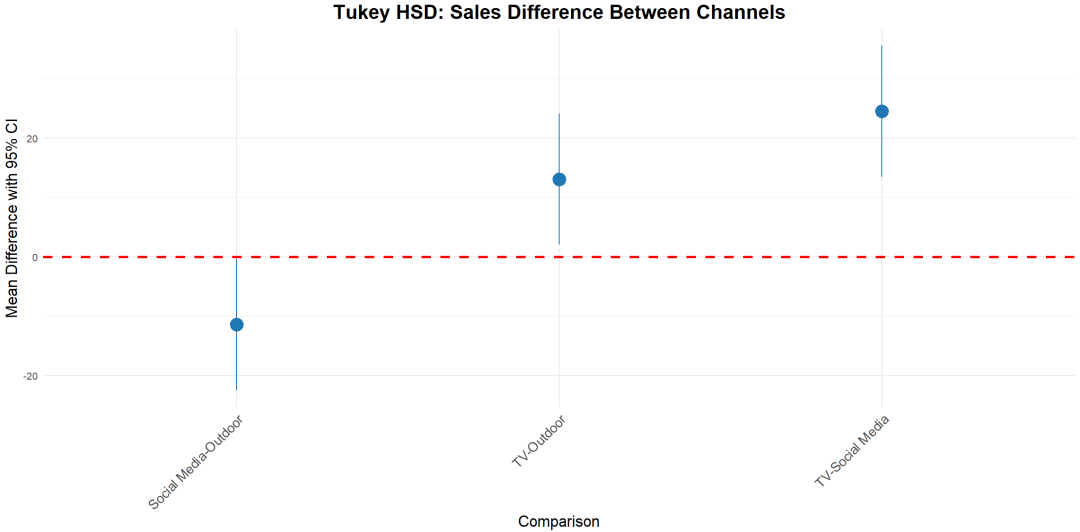
附:关于F值与F检验的说明
理解:与方差分析的概念有复合,方差分析是一种统计检验方法,而F检验是该方法中的一个核心步骤。
定义:方差分析通过分析组间方差和组内方差的比率来判断各组均值是否存在显著差异。
F检验的公式为:
F = 组间方差 / 组内方差
组间方差反映各组均值之间的差异。
组内方差反映同一组内个体之间的差异。
再哆嗦举个例子:
假设我们有三个组的测试成绩,分别为A组、B组和C组。我们希望知道这三个组的均值是否相等。我们可以使用单因素ANOVA来进行检验:
① 计算组间方差:反映A、B、C三组均值之间的差异。
② 计算组内方差:反映每组内部学生成绩的差异。
③ 计算F值:用组间方差除以组内方差。
④ 查F分布表:根据自由度确定临界值。如果F值大于临界值,则说明三个组的均值存在显著差异。