CxHub客户体验社区-用户研究、体验爱好者学习交流社区，专注客户体验(CX)研究。
社交媒体
均值漂移，英文又叫Mean Shift。
均值漂移算法起源于1970年代的密度估计研究，经过多年的发展和完善，特别是在1990年代和2000年代初期，逐渐成为一种重要的非参数聚类方法，并在图像处理和计算机视觉等领域得到了广泛应用。
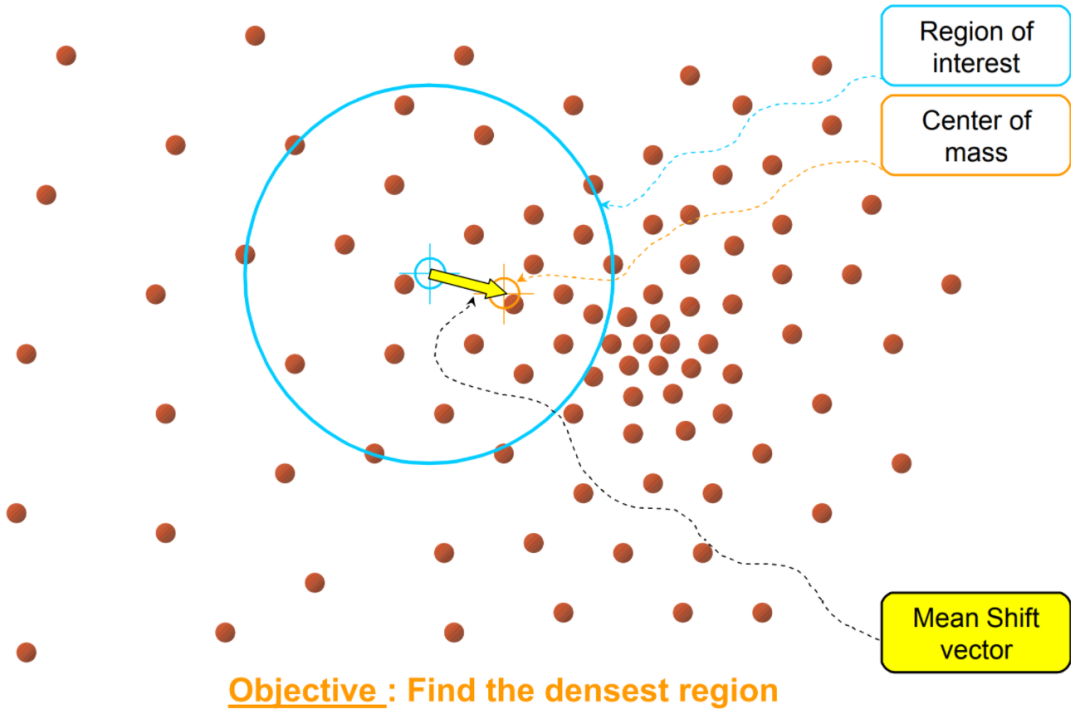
想象我们在一片树林中寻找最密集的树木区域。均值漂移算法就像是盲人用手杖摸索，每一步都朝着手感更密集的地方移动，直到再也感觉不到更密集的区域为止。
对每一个数据点，算法都会估算其周围点的密度表现，然后沿着密度上升的方向移动该点，直至达到密度峰值。
怎么找到密度上升方向？
均值漂移算法的核心步骤是通过计算每个质心在其邻域内的所有点的加权平均，更新其位置。
K-Means算法计算的是所有点的简单平均值，而均值漂移算法则在计算中引入了“加权”，这些权重通过核函数来分配，并利用这些加权值计算新的质心点位置。
① 不需要预先指定簇的数量。
② 能够处理任意形状的簇。
③ 对噪声数据不敏感。
④ 对初始中心点不敏感。
优于传统的K-means等算法。
① 对带宽参数敏感，选择不当可能导致不良聚类。
② 会受到数据分布的影响，在密度差异较大的情况下可能会表现不佳。
③ 可能会在平坦区域或密度相近区域产生伪聚类。
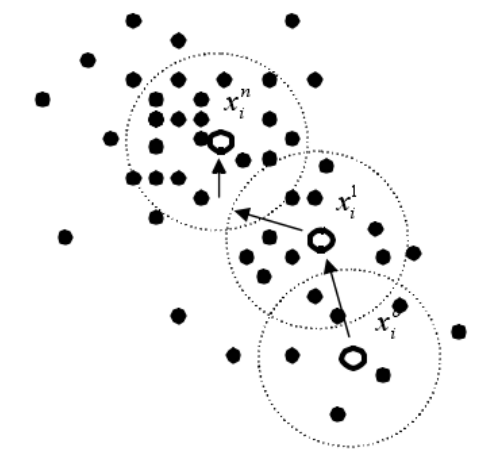
① 确定邻域范围：定义一个半径（带宽）来确定初始点周围的邻域范围。
② 计算平均位置：在邻域范围内，计算所有点的加权平均位置（质心）。
距离质心近的点权重更大，距离远的点权重较小。
③ 移动质心：将质心移动到计算得到的平均位置。
④ 重复步骤：以新的质心为中心，重新确定邻域范围，计算新的平均位置，并再次移动质心。
⑤ 停止条件：当质心的位置变化小于某个预设的阈值时，算法停止。
这时质心就表示一个数据点密集区域的中心。
① 标准化：对变量数据进行数据标准化。
② 分布连续性：由于算法依赖于密度估计，它更适合于样本分布较为连续的场景。
③ 距离有定义：对数据点之间的距离度量有明确的定义，通常采用欧几里得距离。
④ 数据稠密：数据中应该有足够多的点，具有明显的密度峰值区域，噪声也应尽可能少。
⑤ 参数选择：均值漂移算法的性能在很大程度上依赖于邻域范围的选择。
Python的scikit-learn库。
R语言中的meanShiftR包。
MATLAB等。
老习惯，以R为例。
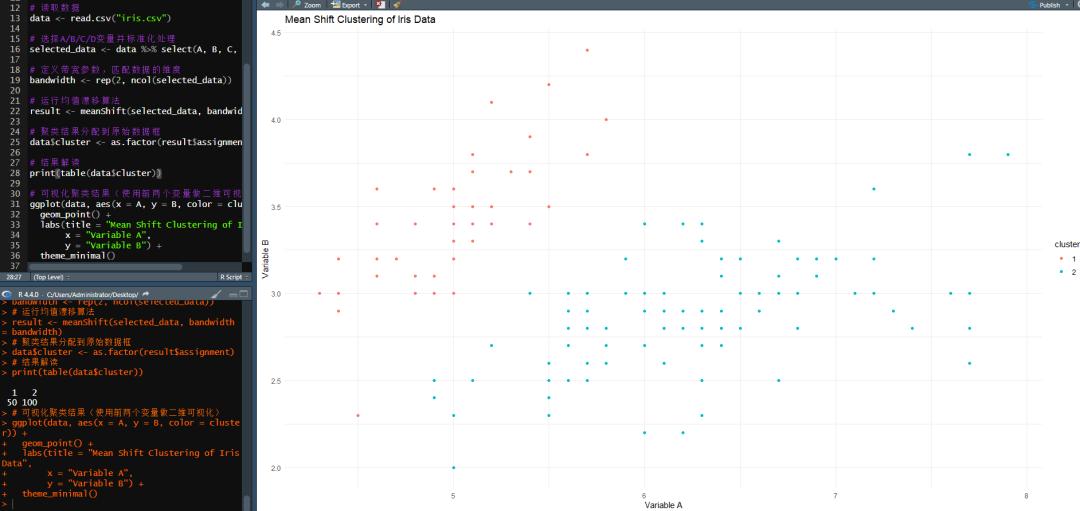
通过R实现均值漂移大概有三种方法
① meanShiftR包：这是一个专门用于均值漂移算法的包，提供了相对直接的接口来执行均值漂移聚类。
② EBImage包：是一个图像处理包，主要用于生物图像分析，但它也实现了均值漂移算法，尤其适用于图像分割任务。
③ 自定义实现：这是最复杂的方法。如果上述包不满足需求，或者需要更大的灵活性，可以根据具体需求进行定制。
实质上，均值漂移算法不像K-means那样广泛使用，因而在一些主流机器学习包中可能没有直接实现。而且有些包虽然实现了均值漂移算法，但主要用于特定领域（如生物图像处理），而不是一般的聚类任务。
与其他聚类算法一致。
可以通过轮廓系数等指标来评估聚类质量，或者采用外部标准进行评估。
① 市场细分：识别不同消费者群体，根据消费行为进行聚类。
② 图像处理：用于图像分割和特征提取，通过聚类相似的像素颜色，将图像分割成几个有意义部分。
③ 社交网络分析：分析社交媒体数据，识别出影响力较大的用户群体，进行精准营销。
④ 生物信息学：基因表达数据的聚类分析。
① 自适应均值漂移：一种改进的均值漂移算法，能够根据数据自动调整带宽，提高聚类效果。
② 在线均值漂移：用于处理流数据的变体，适应实时数据处理的需求。
以上两种需自行探索。
是一种计算两个数据点之间相似性的函数。它实际上是通过某种非线性映射，将数据从低维空间映射到高维空间。在这个高维空间中，原本可能非线性可分的数据有可能变得线性可分。
可以将其类比于衡量人与人之间关系亲疏的指标。
① 线性核：就像直接衡量两个人共同兴趣的数量。共同兴趣越多，关系越亲近。
② 多项式核：类似于考虑共同兴趣的层次和深度。例如，两个人不仅有共同兴趣，还在这些兴趣上有深入的理解和共同的活动。
③ 高斯核：可以想象成在一个多维的“兴趣空间”中衡量两个人的兴趣相似度。在这个空间里，每个人都有一个表示其兴趣的坐标。高斯核函数通过计算两个坐标之间的距离来确定他们的兴趣相似度。距离越近，表示他们的兴趣越相似，关系越亲近。
向量漂移！
核函数加权和向量漂移是同一过程的两个视角：
① 核函数加权视角：我们通过核函数计算权重并进行加权平均，得到新的质心位置。
② 向量漂移视角：我们计算漂移向量，并根据这个向量更新质心位置。
这两个视角是等价的，加权平均提供了一个直观的解释，即新位置是所有点的加权和；而向量漂移则突出了质心移动的方向和步长。
取决于具体的数据集和问题背景。以下是一些影响算法表现的因素：
数据分布：
① 如果数据在高维空间中有明确的密集区域，均值漂移算法可能表现良好。
② 如果数据高度稀疏且噪声较多，均值漂移算法可能表现不佳。
核函数和带宽选择：
① 合适的核函数和带宽选择能够显著改善均值漂移算法在高维数据上的表现。
② 自动化带宽选择方法可以在一定程度上缓解带宽选择的难题。
优化策略：
① 使用近似算法或降维技术（如PCA）可以减少计算复杂度，提高算法在高维数据上的效率。
