CxHub客户体验社区-用户研究、体验爱好者学习交流社区，专注客户体验(CX)研究。
社交媒体
文/小只
在市场与用户研究领域，我们时常面对这样的难题：消费者到底更喜欢哪款产品？用户对最新功能的反馈是否超越了之前的版本？为了得出这些关键结论，我们不仅依赖数据，还需要确保数据背后的结论是真实可信的。
而不是因为偶然或随机波动引发的误判。
假设检验，便是在这一过程中起到关键作用的工具。
它用来判断我们在数据中看到的差异或效果是否显著到足以相信它们是真实存在的，而不是随机误差造成的。
简单来说，它帮助我们厘清“事实”与“偶然”。
它可以告诉我们，两组或多组数据之间的差异是否真的存在，还是仅仅因为随机性造成的虚假现象。
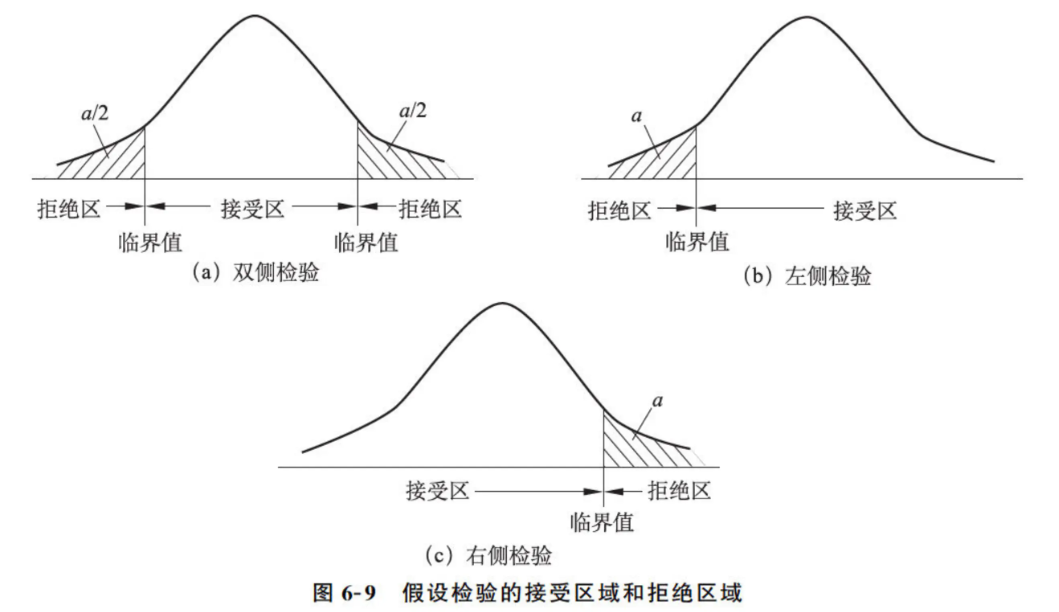
提出假设：
零假设(Null Hypothesis, H0)：通常表示“没有差异”或“没有效果”的假设。
比如说，新包装和旧包装的销量表现相同，广告活动没有对销售产生显著影响。
备择假设(Alternative Hypothesis, H1)：与零假设相对，它表示我们期望看到的差异或效果确实存在。
也就是说，新包装更受欢迎，广告活动显著提升了销量。
假设检验的目标就是通过数据来决定是否有足够的证据拒绝零假设，从而接受备择假设。
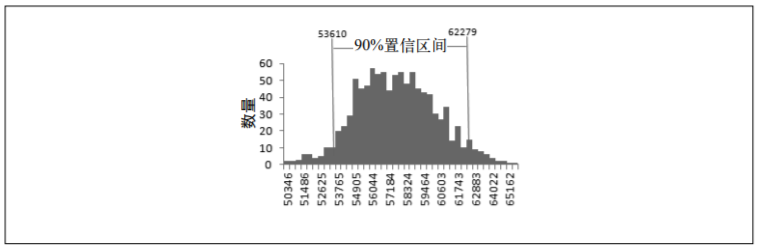
在假设检验中，有一个至关重要的概念——P值（p-value）。
P值代表在假设零假设为真的情况下，观察到当前数据结果或更极端结果的概率。
说白了，P值越小，意味着数据结果越不可能是偶然的，越有理由怀疑零假设不成立。
P值 < 0.05：通常认为结果具有统计学意义，这意味着有95%的信心认为差异是真实存在的。
P值 ≥ 0.05：则表示没有足够的证据来否定零假设，差异可能是随机的，结果无统计学意义。
在市场和用户研究中，显著性检验几乎无处不在。以下是几个经典的应用场景：
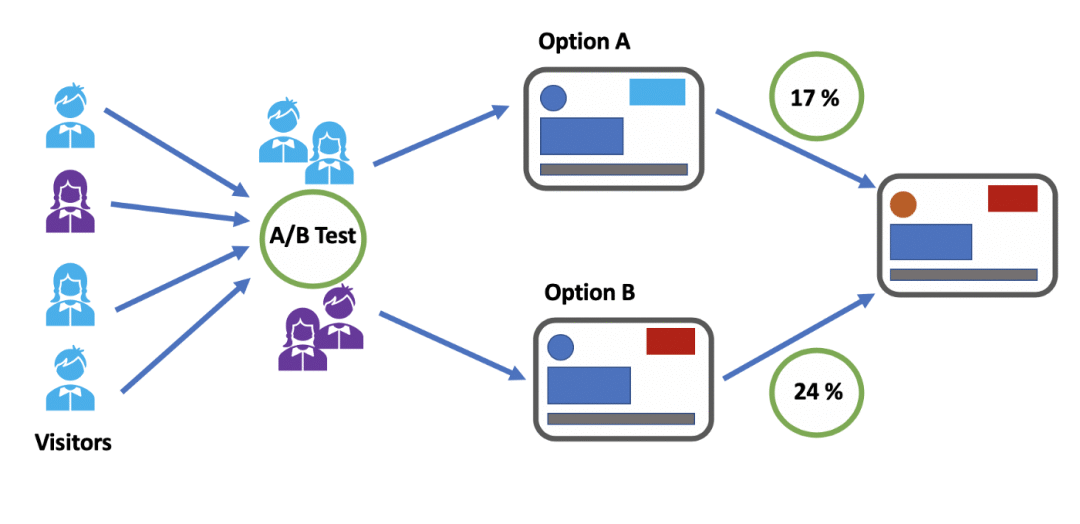
A/B测试：产品或广告效果的“试金石”
A/B测试可以说是研究者的日常工具，它用来比较不同版本的产品、广告或网页设计哪个更有吸引力。
例如，可能想知道新广告是否比旧广告更能吸引用户点击，于是将用户随机分成两组，一组看到新广告，另一组看到旧广告，然后统计每组的点击率。
这时候，显著性检验就能帮助判断新广告和旧广告之间的点击率差异是否足够显著。如果P值很小（比如 < 0.05），可以自信地说，新广告比旧广告效果更好，值得大规模推广。
消费者偏好调查：让选择有依据
当想知道消费者更喜欢哪种产品包装、口味或设计时，通常会进行问卷调查或消费者测试。
比如说，设计了两种不同的包装，想知道哪种更受欢迎。
显著性检验可以分析消费者的反馈数据，判断两种包装的偏好差异是否显著。如果P值很小，这意味着这种差异很可能不是偶然的，可以选择更受欢迎的包装进行生产和推广。
市场细分中的差异分析
在市场细分研究中，我们经常需要分析不同消费者群体之间的差异，比如消费习惯、产品偏好或价格敏感度。
例如，可能想知道男性和女性在购买同一产品时是否表现出显著的价格敏感度差异。
通过显著性检验，可以确定这些差异是否足够显著，从而帮助制定更精准的市场策略，比如为不同性别的消费者设计差异化定价。
样本量的重要性：适量才能显效
样本量是假设检验的基础之一。样本量过小可能导致检验无法发现真实存在的差异，即“假阴性”；
而样本量过大又可能使得统计检验发现一些实际无意义的微小差异，即“假阳性”。
适量样本：设计调研或实验时，确保样本量足够大以检测到实际存在的差异。但也不要盲目扩大样本量，避免数据解读中过度放大无意义的差异。
多重检验问题：小心“假象”陷阱
在研究中，如果你对多个变量或多个组合进行假设检验，可能会面临“多重检验问题”。
多次检验增加了发现假阳性的概率，也就是你可能错误地认为某些差异具有统计学意义。
校正方法：为避免多重检验问题，你可以采用Bonferroni校正等方法，调整显著性水平，降低错误发现的概率。
统计显著性 ≠ 实际意义
统计显著性并不一定意味着实际有意义。
在市场和用户研究中，数据结果即便在统计上显著，仍然需要评估其实际业务价值。
例如，广告点击率提高了0.1%，虽然统计显著，但这对实际销售或品牌提升可能没有实质影响。
结合业务背景：在解读显著性检验结果时，不仅要关注P值，还要结合业务背景评估差异或效果是否具有实际意义。
检验的前提条件：不满足，结果等于零
假设检验基于一定的统计前提条件，如样本独立性、数据的正态分布、方差同质性等。在应用显著性检验之前，确保这些条件得到了满足，否则结果可能会误导决策。
预检验分析：在进行显著性检验之前，可以进行一些预检验分析，如分布分析、方差齐性检验，确保数据符合显著性检验的前提条件。
对于市场研究从业者来说，显著性检验并不需要高深的统计学背景，通过一些常用工具（如Excel、SPSS、R或Python），就能轻松上手。
附：对一些常见的误解做解释
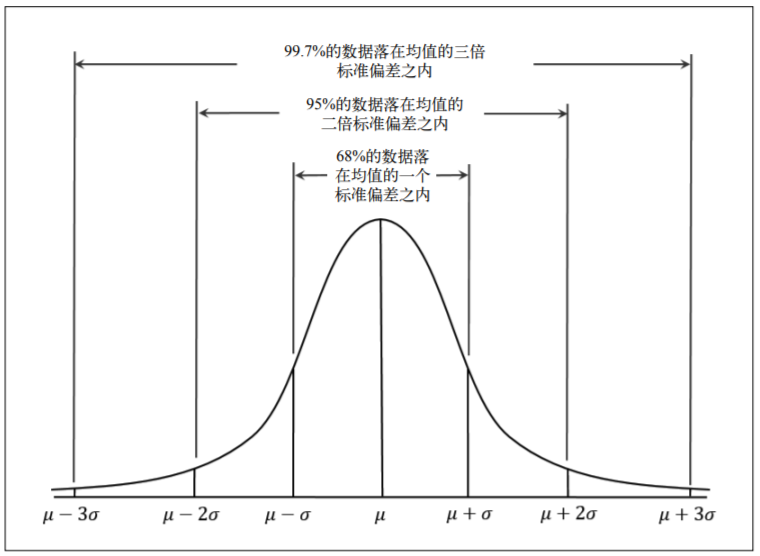
“单次抽样的样本量越大，样本均值等统计量也会趋于正态分布”
明明我的调研只抽样了一次，为什么会有统计量，为什么会趋于正态分布？
澄清点：
单次抽样的样本均值只是一个值，并不会有分布。
如果重复抽样，随着样本量的增加，样本均值的分布会趋向于正态分布，这是基于中心极限定理的。
在单次抽样中，样本量越大，样本均值更接近于总体均值，误差更小，推断更可靠。这不是因为单个样本均值本身有分布，而是因为大样本更能代表总体的多样性和复杂性，降低了抽样误差。
