
线性回归是数据分析领域中最基础且广泛应用的工具之一。
它不仅在统计学中占据重要位置,也是用户研究、市场分析中常见的预测与决策支持工具。
线性回归(Linear Regression)是一种用于描述变量之间线性关系的统计方法。
它通过找到自变量(解释变量)与因变量(目标变量)之间的最优线性关系,来预测目标变量的值。
线性回归模型的核心思想是:在一组已知数据中,寻找一条直线,使得该直线尽可能接近所有数据点,并能够预测新的数据。
线性回归模型通常以以下形式表达:
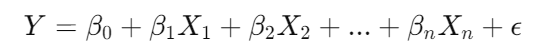
Y:因变量,即我们想预测的目标值(如销售额)。
X₁, X₂, ... Xₙ:自变量,即我们用于解释因变量变化的变量(如广告费用、市场推广预算等)。
β₀:截距,表示当所有自变量为0时,因变量的估计值。
β₁, β₂, ... βₙ:回归系数,表示自变量对因变量的影响,即每个自变量增加一个单位,因变量的平均变化量。
ε:误差项,表示数据中的随机误差或未解释的部分。
线性回归的核心算法是最小二乘法(Ordinary Least Squares, OLS)。
它的目标是通过最小化预测值与实际值之间的差距平方和,来拟合出一条最优直线。
简单来说,最小二乘法试图找到那条“最佳”直线,使得实际数据点到该直线的距离(残差)之和最小化。
① R²值(决定系数)
是评估线性回归模型优劣的关键指标。它表示模型解释因变量变化的比例。
R²越接近1,说明模型解释力越强。
R² = 1:模型完美解释数据变化。
R² = 0:模型无法解释数据变化。
②回归系数显著性检验
这是对回归模型中每个自变量的回归系数进行的显著性检验(通常通过 t 检验)。
其目的是检验每个自变量对因变量的影响是否显著。
③ 整体回归方程显著性检验
整体回归模型的显著性检验通常通过 F 检验来实现,用于判断整个模型是否显著。
F 检验可以解释整体模型的有效性。
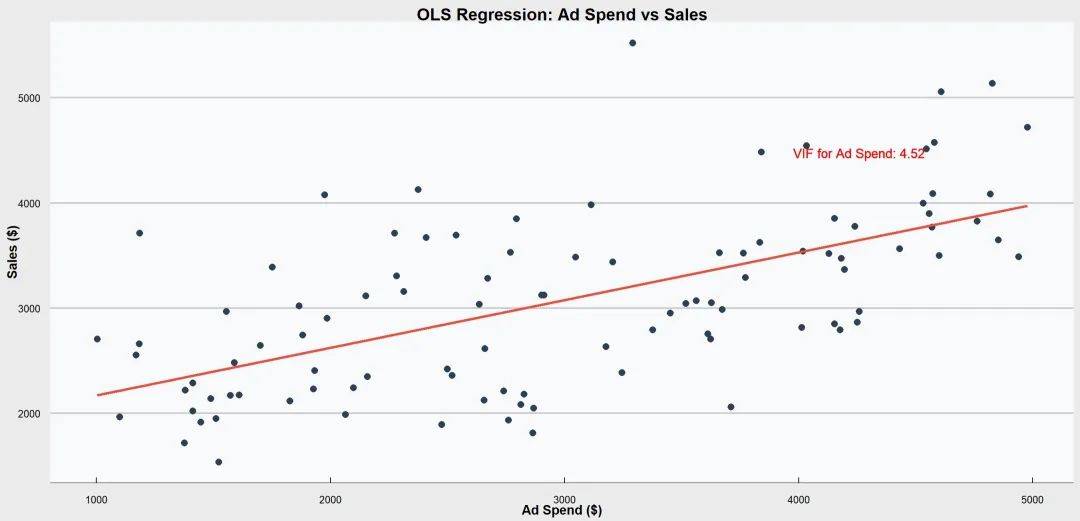
① 简单线性回归
是回归分析中最基础的一种形式。
主要目的是通过一个自变量(预测变量)来预测因变量(响应变量)的值。
这个过程假设这两个变量之间存在线性关系,即它们可以通过一条直线来近似描述。
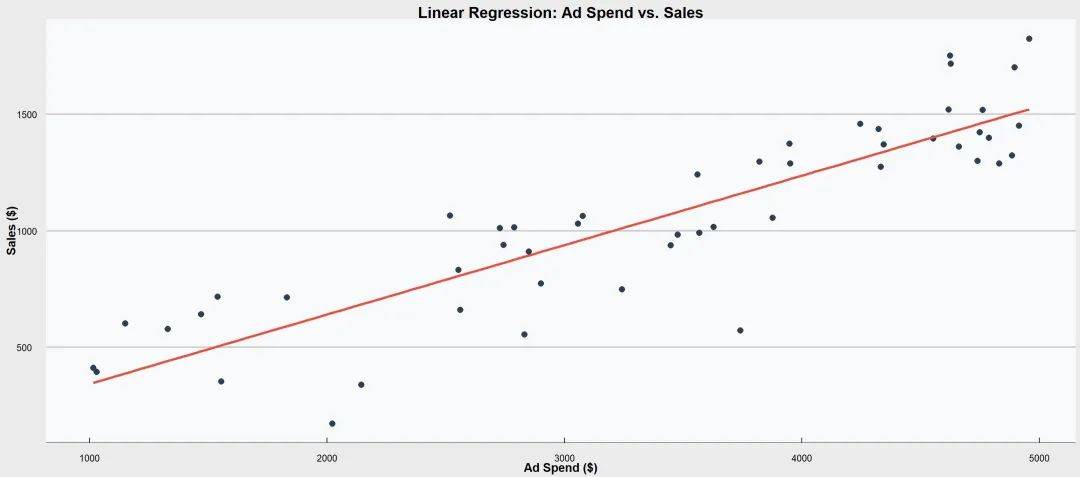
② 多元线性回归
是简单线性回归的扩展,允许使用多个自变量来预测一个因变量。
多元线性回归模型的目标是找到每个自变量的最佳回归系数,使得预测值与真实值之间的误差最小化。
通常这个过程通过最小二乘法来实现。
③ 正则化回归
当模型中的自变量数量过多,或者自变量间存在高度相关性时,线性回归模型容易出现 过拟合 问题。
过拟合意味着模型在训练数据上表现很好,但在测试新数据上表现不佳。
正则化的核心思想是向模型的损失函数中添加一个惩罚项,该惩罚项用来限制模型的复杂度。
通过惩罚参数的大小,正则化迫使模型不要过度依赖每一个特征,鼓励模型通过较少的特征(或较小的权重)去拟合数据,从而获得更简洁和泛化能力更强的模型。
Ridge回归(L2正则化)
通过在损失函数中增加一个惩罚项来缩减回归系数的大小,可以减少系数的波动,不会完全将某些回归系数缩为零。
Lasso 回归(L1正则化)
采用回归系数的绝对值作为惩罚项,具有自动选择变量的功能,即它能够将某些回归系数缩为零,从而剔除不相关的变量。
弹性网回归(Elastic Net)
结合了岭回归和Lasso回归的优点,通过在损失函数中同时引入L1和L2正则化项。
提供了比Lasso更稳定的变量选择结果。
对于复杂的高维数据,弹性网往往优于单独的岭回归或Lasso回归。
需要调参选择 λ1和 λ2,计算复杂度更高。
④ 广义线性模型(GLM)
这部分后续篇章会再做介绍
在线性回归中,因变量被假设为服从正态分布,且自变量和因变量之间的关系是线性的。
然而,在许多实际问题中,这些假设可能不成立。例如,二分类问题中的因变量只能取0或1。
广义线性模型(GLM)是线性回归的进一步推广,允许我们对非正态分布的因变量进行建模。
常见的GLM类型有Logistic回归、Poisson回归、Gamma回归等。
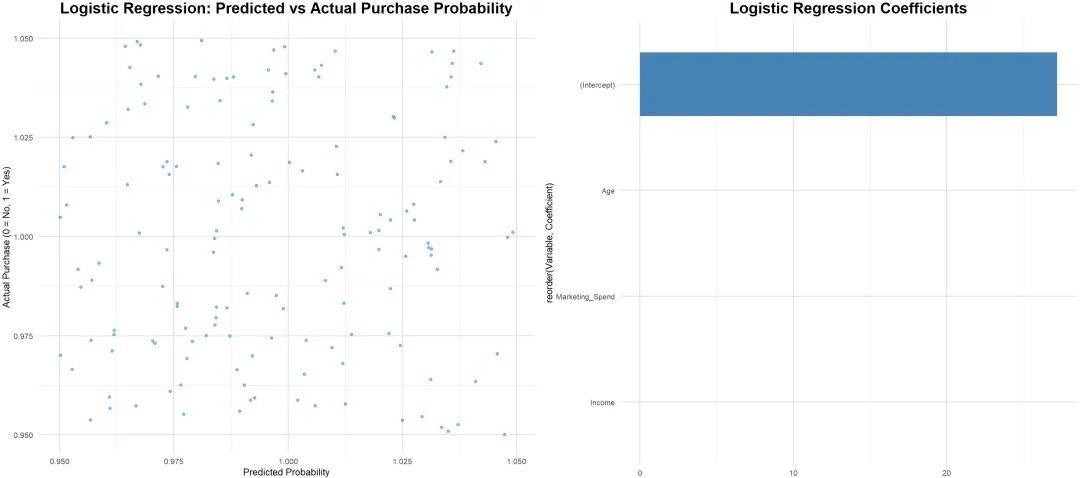
① 线性假设
自变量与因变量之间的关系是线性的,即可以通过直线方程来拟合。
检验方法:描绘散点图判断即可。
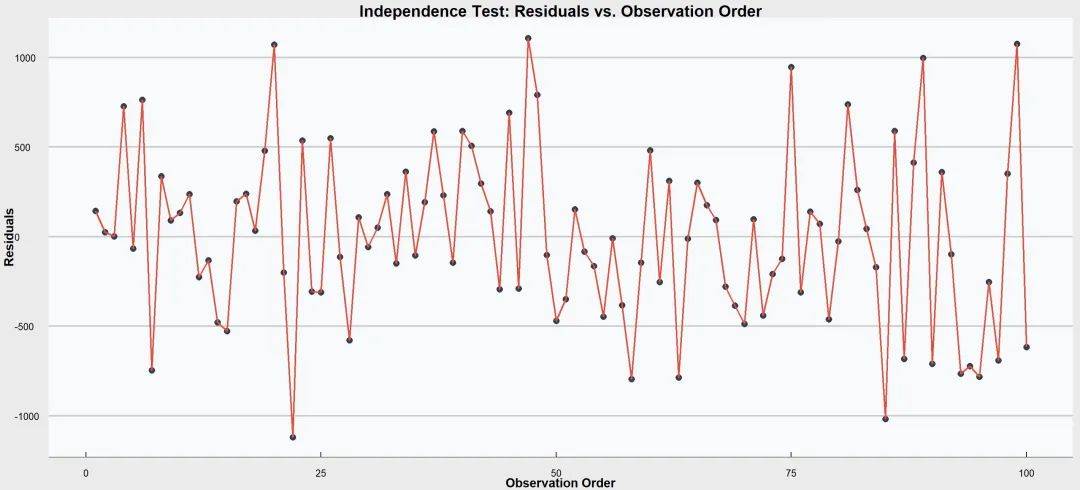
② 独立性
观测值之间的独立性,即每个观测值的残差应当相互独立。
这意味着一个观测值的误差不应影响其他观测值的误差。
检验方法:
① 绘制残差自相关图,随机分布最好。
② 统计检验:Durbin-Watson检验。
专门用于检测序列数据中残差的自相关性。检验结果的值在0到4之间,接近2表示无自相关,低于1或高于3则可能存在自相关。
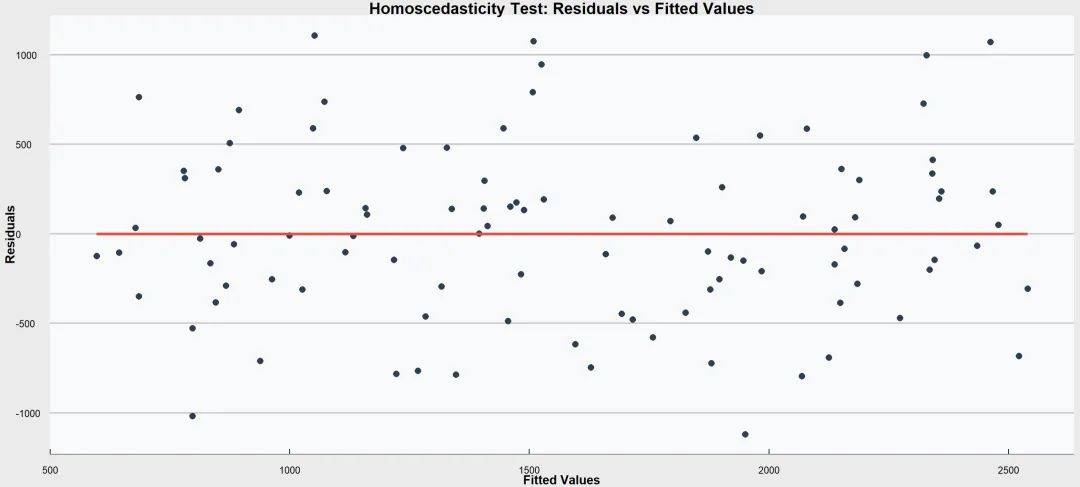
③ 同方差性
残差(预测值与实际值之间的差异)的方差应该在所有自变量的取值下保持恒定。
检验方法:
① 绘制残差图
将残差与预测值作图。如果残差在图中呈现出一种随机分布,说明满足方差齐性。
② 统计检验
通过线性回归的【ANOVA】表的Sig值判断,小于0.05为方差齐性,大于0.05为方差不齐。
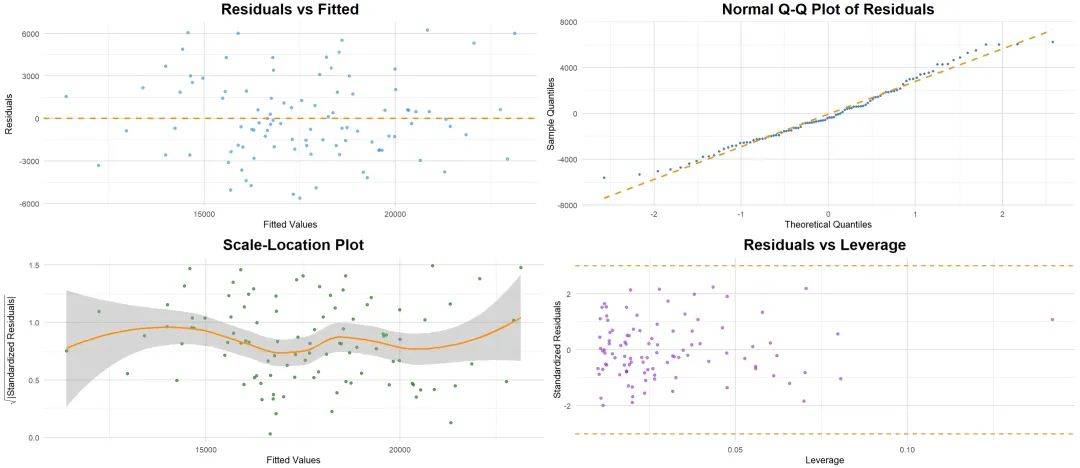
④ 正态性
残差(即实际值与预测值之间的差异)的分布应接近正态分布。
这意味着残差的分布在均值附近对称,且大多数残差应接近于零。
检验方法:
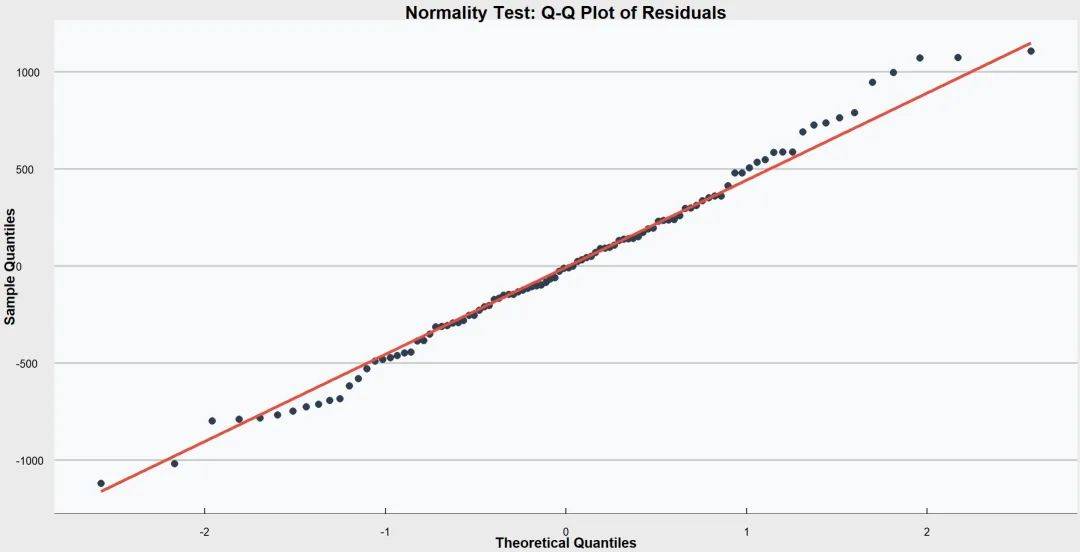
① QQ图/PP图
将残差的分位数与正态分布的分位数作图。
如果残差点沿着45度线分布,说明残差接近正态分布。
② 直方图
绘制残差的直方图,观察其分布形态是否接近正态分布。
③ Shapiro-Wilk检验
专门用于检验样本是否来自正态分布,p值小于显著性水平(如0.05)表示拒绝正态性假设。
④ Kolmogorov-Smirnov检验
另一种常用的检验方法,比较样本分布与正态分布的差异。
⑤ 正态性转化
如果残差不满足正态性,可以考虑对因变量进行转换(如对数转换)以改善正态性。
⑤ 共线性诊断
自变量之间是否存在高度相关性,适用于多元线性回归。
检验方法:
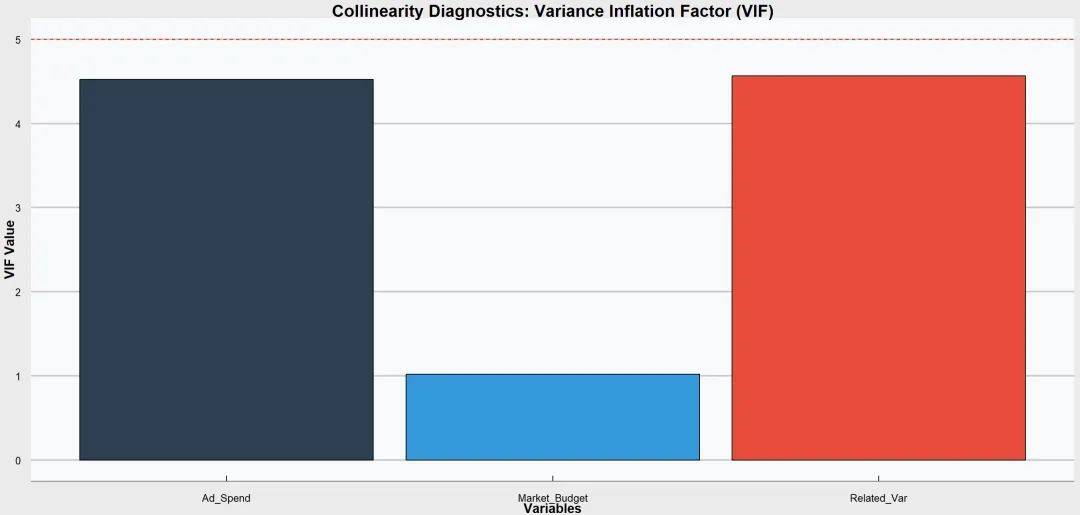
① 方差膨胀因子(VIF)
计算每个自变量的VIF值,膨胀因子越接近1,多重共线性越弱,通常VIF值大于10表示存在显著的共线性。
② 条件数
计算自变量矩阵的条件数,值大于30通常表明存在严重的共线性。
③ 相关矩阵
检查自变量之间的相关系数,若某些变量之间的相关系数接近1或-1,说明存在共线性。
① 忽视残差分析
在使用线性回归模型时,仅仅依赖R²值是不够的。残差分析能够帮助我们判断模型是否适用于数据,以及是否存在模型拟合问题。
前文有讲述,不再展开。
② 忽略自变量间的多重共线性
当多个自变量之间有强相关性时,模型的回归系数可能会变得不稳定,难以解释。
③ 只能处理线性关系
线性回归只能捕捉线性关系,无法有效处理非线性关系。
④ 对异常值敏感
线性回归对数据中的异常值(outliers)非常敏感。一个或几个异常值可能会极大地影响模型的拟合效果。
⑤ 过度拟合
当引入过多自变量时,模型可能会“过拟合”数据,导致在新数据上的预测能力下降。
前述的正则化方法有助于防止过拟合。
① 数据收集与准备
首先,收集相关的自变量和因变量数据。确保数据质量,去除异常值,并处理缺失数据。
② 数据可视化与探索
使用散点图等工具可视化自变量与因变量之间的关系,初步判断它们是否存在线性关系。
③ 拟合回归模型
使用统计软件或编程工具(如Excel、R、Python)拟合线性回归模型。
对于简单线性回归,工具会自动计算截距和回归系数。
④ 模型评估
通过查看R²值、残差图等方式评估模型的拟合效果。检查是否存在异方差性或多重共线性等问题。
⑤ 预测与解释
使用拟合好的回归模型进行预测,并解释自变量对因变量的影响。