
在数据分析中,对数变换(log transformation)是非常常见的一种技术,它能够帮助研究人员解决多种问题,特别是在数据分析和建模过程中遇到的非线性关系、异常值、异方差性等问题。
为了更好地理解为什么在用户研究中使用对数变换,需要从数据本身的性质、研究目的以及实际应用的背景来逐步分析。
对数变换本质上是对原始数据的数学转换。其基本形式为:
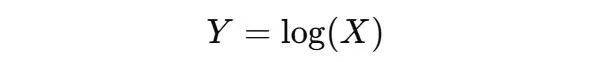
其中:
X 是原始数据,通常是一个正数。
log 代表对数函数,常见的对数底数有自然对数(底数为 e)和以10为底的常用对数。
对数变换能够将大范围的数值压缩到较小的范围,并且减小极端值对分析结果的影响。这种变换使得数值分布更加符合常规的统计假设,比如正态性,或者能让模型更加有效地学习到数据之间的关系。

背景:
在许多实际问题中,数据分布往往是偏态的,即数据的大部分集中在某个区域,而少数数据则分布在远离该区域的地方。右偏分布(正偏)尤为常见,特别是在收入、销售额、用户购买金额等经济类数据中。
案例:
假设我们在分析一款电商平台的用户购买金额数据。数据集包含了10,000名用户,其中大多数用户的购买金额较低,但也有一小部分用户的购买金额非常高,导致数据呈现严重的右偏分布。
原始数据示例:
用户1购买金额:5元
用户2购买金额:10元
用户3购买金额:7元
……(大多数用户的购买金额都在50元以内)
用户9999购买金额:5000元
用户10000购买金额:15000元(极端大值)
原始分布:
很多数据集中在50元以下,少数极大值(5000元和15000元)导致数据右偏。
对数变换后的效果:
对原始购买金额进行对数变换后,数据的分布会变得更加对称,极大值的影响也会得到压缩。
例如,对购买金额进行对数变换(自然对数或常用对数):
用户1购买金额:5元 → 对数变换后:log(5) ≈ 1.609
用户2购买金额:10元 → 对数变换后:log(10) ≈ 2.302
用户3购买金额:7元 → 对数变换后:log(7) ≈ 1.946
……(绝大多数数据值的变动幅度较小)
用户9999购买金额:5000元 → 对数变换后:log(5000) ≈ 8.517
用户10000购买金额:15000元 → 对数变换后:log(15000) ≈ 9.615
变换后的分布:
由于对数变换的压缩效应,极大值对整体数据分布的影响显著减少,数据变得更加对称,整体趋势更加明显。
分析效果:
通过对数变换,原本右偏的购买金额数据变得更符合正态分布,从而能够使用更加适合的统计方法(如回归分析)。模型对低购买金额的用户更加敏感,减少了极高购买金额用户对整体分析结果的扭曲。
背景:
在回归分析中,异方差性指的是随着自变量变化,因变量的方差也发生变化,导致模型的估计不可靠。对数变换能够将因变量的波动性(方差)稳定下来,从而提高回归模型的拟合效果。
案例:
假设我们在分析广告费用对销售额的影响。我们收集了不同广告费用下的销售额数据,但我们发现,广告费用较低时,销售额的波动较大,而广告费用较高时,销售额的波动相对较小。
原始数据示例:
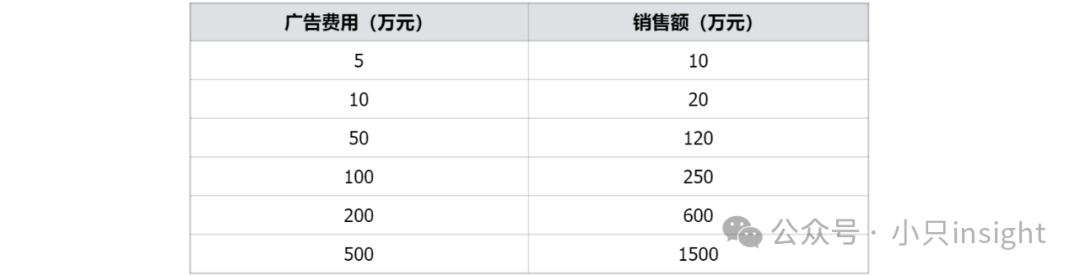
原始数据的异方差性:
广告费用较低时(例如5万和10万),销售额的波动非常大,从10万到20万之间波动,而广告费用较高时(例如200万和500万),销售额的波动相对较小,从600万到1500万的变化幅度较小。
对数变换后的效果:
我们对广告费用和销售额都进行对数变换:
广告费用:log(5) ≈ 0.699,log(10) ≈ 1.000,log(50) ≈ 1.699,log(100) ≈ 2.000,log(200) ≈ 2.301,log(500) ≈ 2.699
销售额:log(10) ≈ 1.000,log(20) ≈ 1.301,log(120) ≈ 2.079,log(250) ≈ 2.398,log(600) ≈ 2.778,log(1500) ≈ 3.176
对数变换后,广告费用和销售额的波动性大大减小,销售额波动性与广告费用的增加趋于一致,即广告费用较低时的销售额波动幅度变小,广告费用较高时的销售额波动幅度增加,整体趋于平稳。
分析效果:
对数变换后,广告费用和销售额之间的异方差性被有效解决,模型可以更好地拟合数据,提高了回归分析的准确性,结果更具解释性。
背景:
在数据中,极端值(离群值)可能对整个分析结果产生不良影响,尤其是当极端值不具备实际意义或可能是数据错误时。对数变换可以将极端值压缩,减少其对分析结果的影响。
案例:
假设我们正在分析一款游戏中用户的单次充值金额。大部分用户的充值金额相对较低,但少数用户进行了一次非常高的充值,导致数据中存在极端值。
原始数据示例:
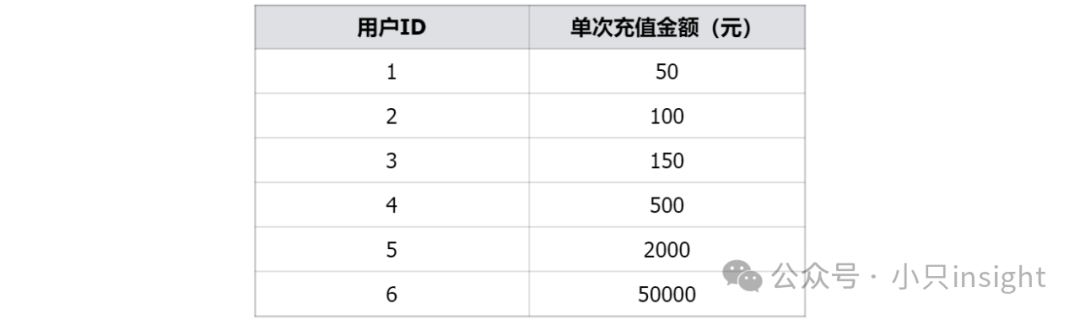
极端值的影响:
用户6的充值金额为50000元,远高于其他用户,这个极端值可能会导致数据分析结果的偏差。原始数据的分析中,这个极端值将对整体结果产生巨大影响。
对数变换后的效果:
我们对单次充值金额进行对数变换:
用户1充值金额:log(50) ≈ 1.699
用户2充值金额:log(100) ≈ 2.000
用户3充值金额:log(150) ≈ 2.176
用户4充值金额:log(500) ≈ 2.699
用户5充值金额:log(2000) ≈ 3.301
用户6充值金额:log(50000) ≈ 4.699
通过对数变换,极端值50000元的影响被显著压缩,充值金额变得更加均匀,分析结果更加稳定。
分析效果:
对数变换后,极端值的影响减小,能够更准确地捕捉到大多数用户的行为特征,从而为产品优化和决策提供更可靠的依据。
④ 改进模型的线性关系
背景:
许多分析模型假设自变量和因变量之间存在线性关系。然而,实际数据中的关系往往是非线性的,特别是在经济学、市场营销等领域。对数变换能够将非线性关系转化为线性关系,从而使得模型更容易拟合。
案例:
假设你正在分析广告费用对销售额的影响。广告费用和销售额之间的关系呈现指数增长的趋势,即广告费用每增加一定比例,销售额会增加更大比例。
原始数据示例:

非线性关系:
广告费用和销售额之间的关系是非线性的,随着广告费用的增加,销售额的增长比例也越来越大。
对数变换后的效果:
我们对广告费用和销售额进行对数变换:
广告费用:log(1) = 0,log(2) ≈ 0.301,log(3) ≈ 0.477,log(4) ≈ 0.602,log(5) ≈ 0.699,log(6) ≈ 0.778
销售额:log(2) ≈ 0.301,log(4) ≈ 0.602,log(6) ≈ 0.778,log(8) ≈ 0.903,log(12) ≈ 1.079,log(15) ≈ 1.176
通过对数变换,广告费用与销售额之间的关系变得更加线性,回归分析可以更准确地捕捉这一线性关系。
分析效果:
对数变换后,非线性关系转化为线性关系,模型更加简单,预测精度提高。
伴随着以上的分析,对数转换的优势和劣势呼之欲出:
优点
① 平滑数据:对数变换能够减小极端值和大数值的影响,使得数据更加平滑,适合进行回归分析。
② 线性化非线性关系:能够将呈现指数增长或幂律分布的关系转化为近似线性关系,便于分析。
③ 处理异方差性:对数变换能有效缓解方差不稳定的问题,特别是在回归分析中,避免不同值范围的数据对模型拟合产生不均衡影响。
④ 优化数据分布:对数变换通常能够使数据更接近正态分布,这对于很多统计方法来说是一个重要前提。
缺点
① 无法处理负数或零值:对数变换只能应用于正数数据,对于包含零值或负数的数据,必须进行其他的处理(如加一个常数)。
② 数据解读难度增加:对数变换后的数据与原始数据的解读会变得不那么直观,特别是在向非专业用户或决策者报告时,可能需要额外的解释。
通过上述分析,可以看出对数变换在解决偏态分布、稳定方差、减少极端值的影响以及改进模型的线性关系方面的强大作用。每个领域的数据都可以根据其特性,通过合理的对数变换得到更优的分析结果。