CxHub客户体验社区-用户研究、体验爱好者学习交流社区，专注客户体验(CX)研究。
社交媒体
在研究中，我们经常需要分析多个因素(例如品牌、性别等)对用户满意度的影响。
如何科学地判断这些因素是否显著影响用户的感受？
多因素方差分析方法就是用来解决这个问题。
多因素方差分析是方差分析的一种扩展，它用于研究两个或以上自变量对1个因变量的影响。
结合上一篇文章来看：
单因素方差分析：只研究品牌对满意度的影响。
多因素方差分析：同时研究品牌和用户性别对满意度的影响。
当实验涉及多个影响因素，并且想知道这些因素是独立影响，还是有交互作用。
某个因素的影响会随着另一个因素的变化而变化的时候。
后面的讲述可能会存在很多不同的名词，先来简单科普一部分：
因素：实验中的变量(如性别、品牌)。
水平：因素的具体分类(如性别分男、女两个水平)。
主效应：单个因素对结果的影响(如性别本身的影响)。
交互作用：因素组合产生的特殊效果(如性别×品牌的叠加影响)。
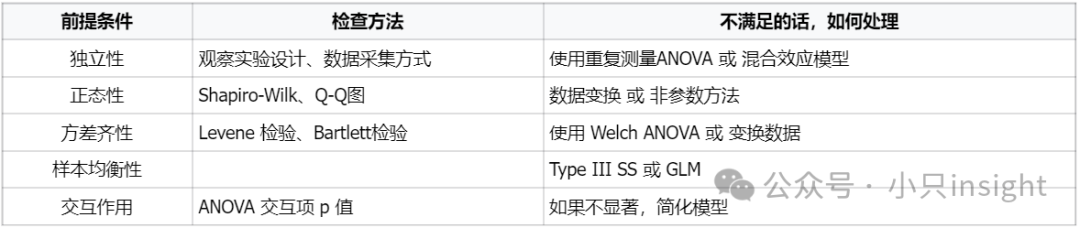
如果以下假设满足，可以进行标准的多因素方差分析。
如果以下假设不满足，则需要使用适当的方法进行调整。
我们想研究：
不同品牌的手机(A、B、C)是否影响满意度？
性别(男性、女性)是否影响满意度？
品牌和性别是否有交互作用？
即某个品牌的满意度是否在不同性别间存在显著差异。
调查了30名用户，收集他们对手机满意度评分(1-10分)，数据如下：
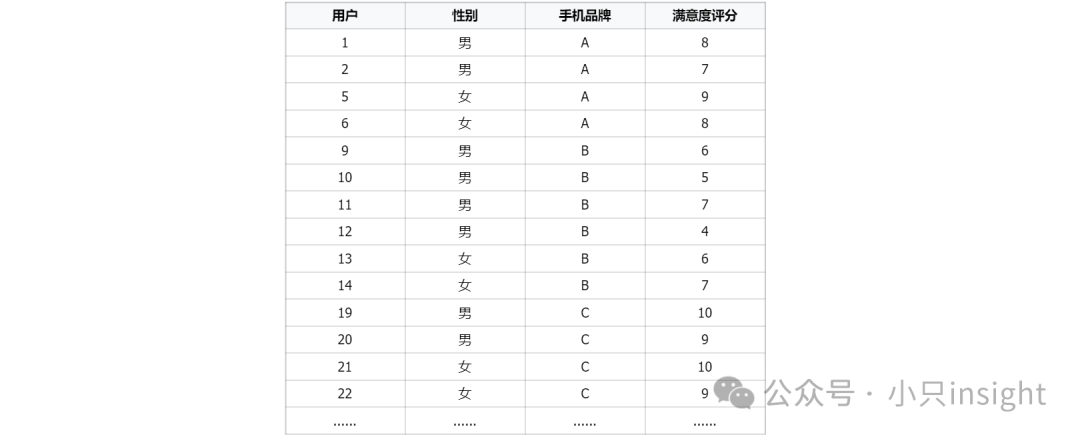
然后在SPSS中进行多因素方差分析，分析这两个因素(品牌、性别)是否影响满意度。
此处略。
点击分析→常规线性模型→单变量。
因变量：满意度。
固定因子：品牌、性别。
勾选均值比较，以查看不同组的均值。
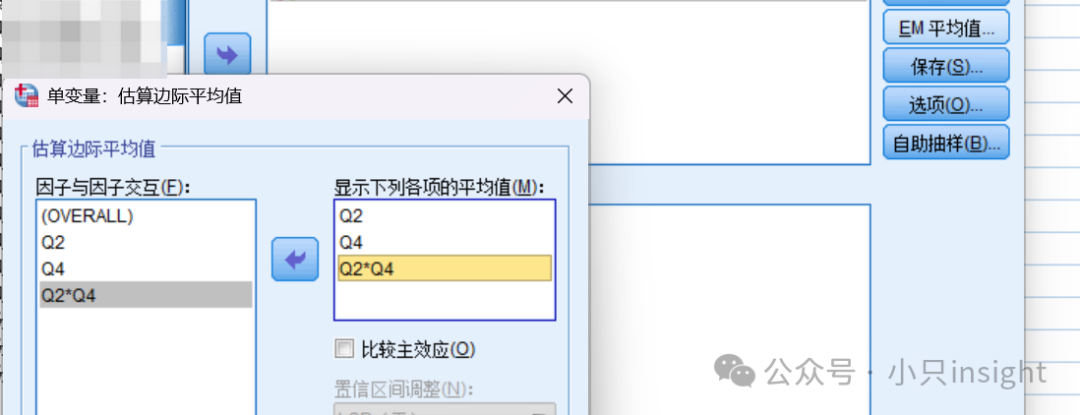
勾选事后检验，选择LSD或Bonferroni，查看不同水平间的具体差异。
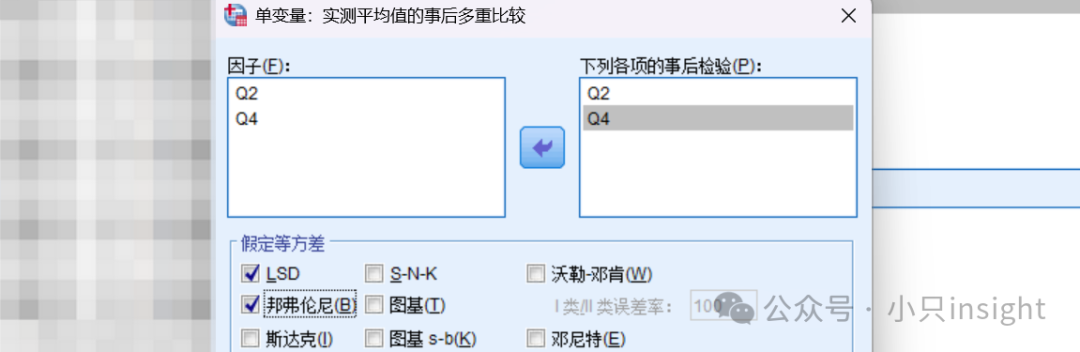
点击模型→选择全因子模型。
勾选描述统计、效应量估算、齐性检验。
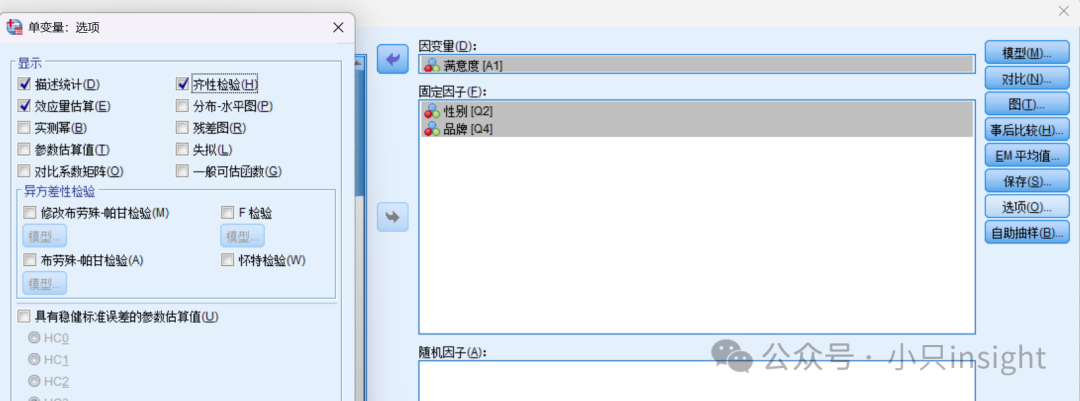
点击OK，运行分析。
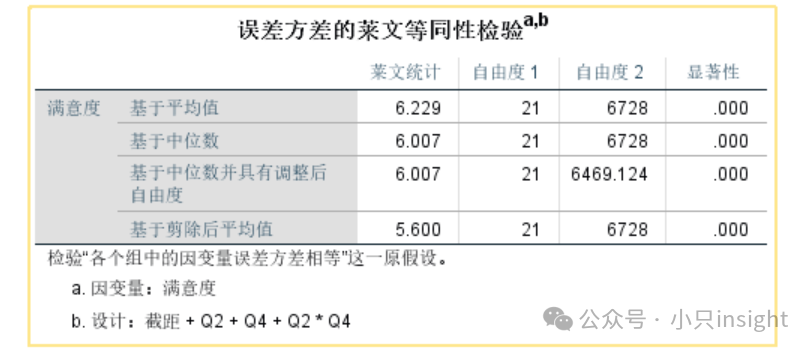
莱文检验结果：用于检验各组的误差方差是否相等，即方差齐性假设。
如果p值很小，意味着我们拒绝方差齐性假设，认为各组误差方差不相等。
莱文统计值： 第一列给出了不同计算方法下的莱文检验统计量，它衡量各组的方差差异。
如果数值较大，表示组间误差方差的差异较大。
显著性(p值)：所有方法p值均为0.000。
这意味着拒绝原假设，即误差方差不相等，不满足方差齐性假设。
拓展：
莱文检验可以基于不同的统计方法进行计算：
基于均值(最常用)：假设数据分布接近正态时，使用均值计算方差。
基于中位数：对极端值更稳健，适用于数据分布偏斜或有异常值的情况。
基于中位数并调整自由度：进一步调整自由度，使得检验更加稳健。
基于剪除后均值：去掉极端值(如删除数据中的前5%和后5%)，减少异常值的影响。
目前所有方法的p值都为0.000，无论使用哪种方法，都表明误差方差不相等。
分析解读
修正模型的F值为13.621，p<.001，表明整体模型显著。
说明选取的变量对整体满意度有显著影响。
但偏Eta平方为0.041，表明解释的方差比例较小(4.1%)。
Q2变量(F=0.015,p=.903)对整体满意度无显著影响，偏Eta平方为0.000，说明Q2的解释力可以忽略。
Q4变量(F=26.870,p<.001)对整体满意度有显著影响，偏Eta平方=0.038，说明Q4解释了3.8%的方差，影响较小但显著。
Q2*Q4交互作用(F=1.381,p=.182)不显著，说明Q2和Q4之间的交互效应不影响整体满意度。
如果显著，可以考虑通过按不同水平进行多次单因素方差分析来看相互之间的显著性。
拓展：
如果一个因子F值显著，但偏ETA平方很小，说明虽然该因子有统计学意义，但它对因变量影响很弱。
如果一个因子F值显著，且偏ETA平方很大，说明该因子不仅显著，且影响很大。
偏ETA平方的取值范围
0≤偏ETA平方≤1
一般来说，取值范围和解释如下：
0.01≤偏ETA平方<0.06：小效应
0.06≤偏ETA平方<0.14：中效应
偏ETA平方≥0.14：大效应
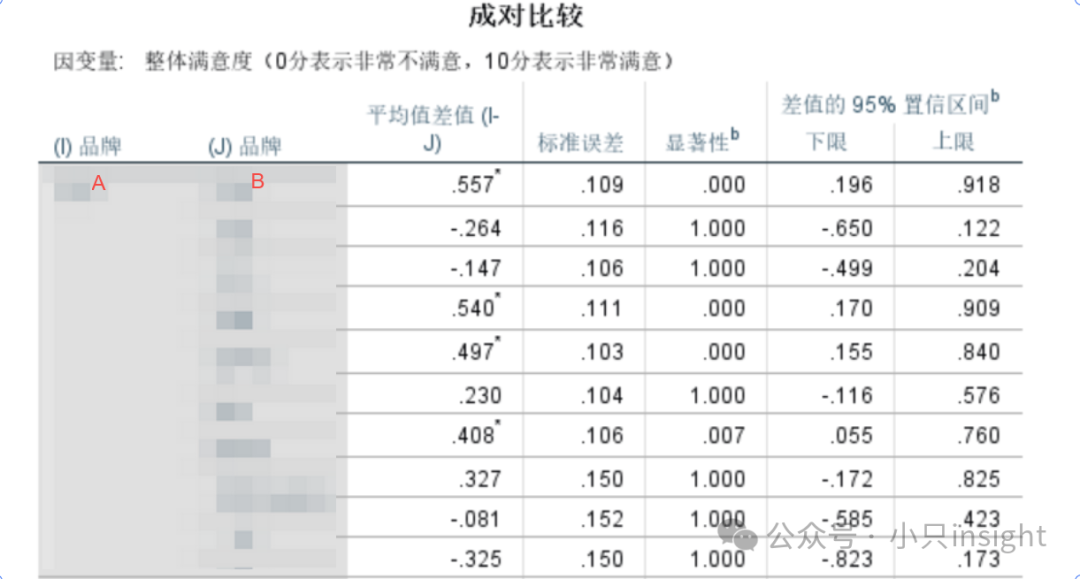
分析解读
P值若<0.05，说明差异显著。
若置信区间包含0，则表明品牌间无显著差异。
A和B之间均值差值=0.557，p=0.000(显著)，说明A的整体满意度显著高于B。
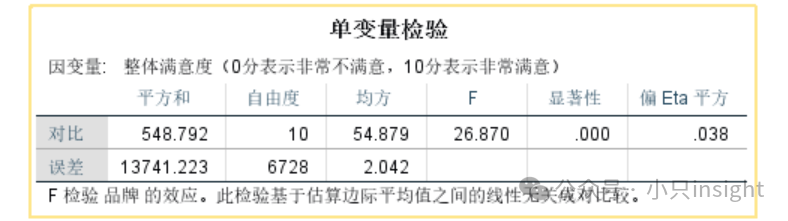
分析解读
品牌的F值=26.870，p=0.000，说明品牌对整体满意度有显著影响。
偏Eta平方=0.038，说明品牌解释了3.8%的满意度变异，影响力较小。
说明满意度的影响因素不止品牌，还可能涉及用户体验、售后服务等其他因素。
不做重复分析解读，可参考成对比较表。
注意点：在多因素方差分析中，SPSS只会做主效应的成对比较，而不会自动执行交互效应的简单效应分析，需要用语法实现或者做多轮单因素方差分析。
这一点是真不科学。
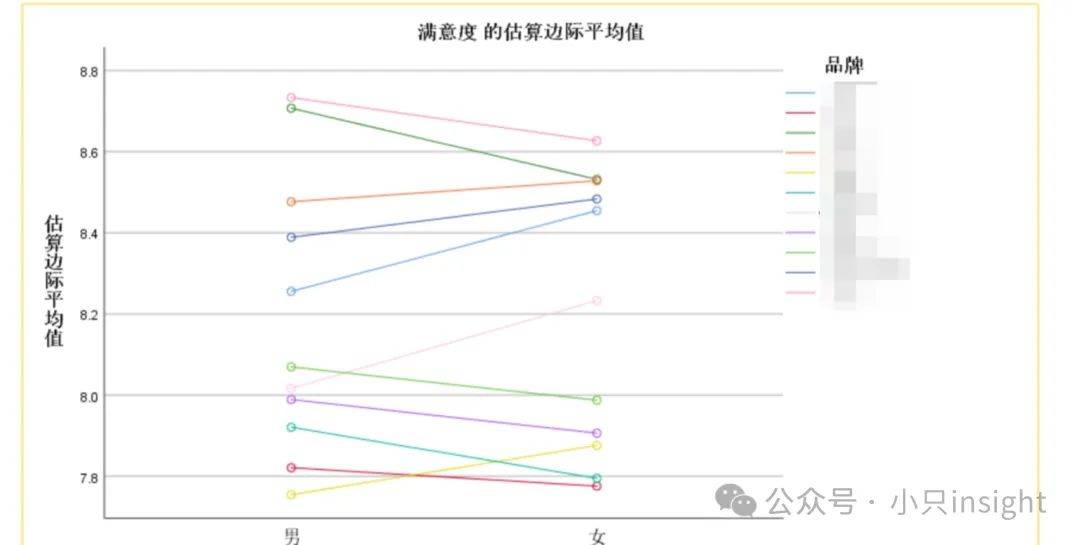
分析解读：
这个轮廓图核心作用是直观展示交互效应，并帮助理解不同变量之间关系。
图中体现 ：
若不同品牌的满意度趋势线平行 ，则说明性别与品牌无交互效应(仅主效应存在)。
若趋势线交叉或发散，则说明性别与品牌存在交互效应(即同一品牌在不同性别中的表现差异显著)。
比较组间差异，通过线条高低和斜率，快速识别不同品牌在男女群体中的满意度差异。
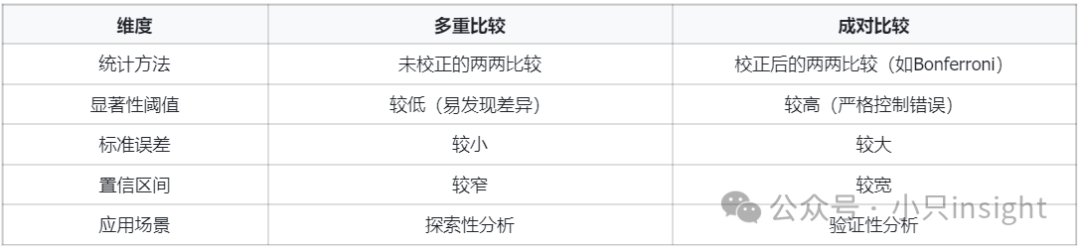
建议结合两种结果 ：若多重比较和成对比较均显著，结论更可靠；若仅多重比较显著，需考虑是否为偶然差异。
以上。
