问题切入

我有6个不同维度下的满意度评价的变量，我也有一个手机A的变量，我想看看机型A在不同维度下的满意度评价之间有没有显著性差异，怎么做呢？

这类数据的统计分析，常用的方法之一便是单因素重复测量方差分析。

当实验中只有一个重复测量的自变量（因素），即同一组样本在多个时间点或多个条件下接受测量。

听着是不是挺熟悉的，跟配对t检验有点像。

用一张图来简单说明差异：

关键点：

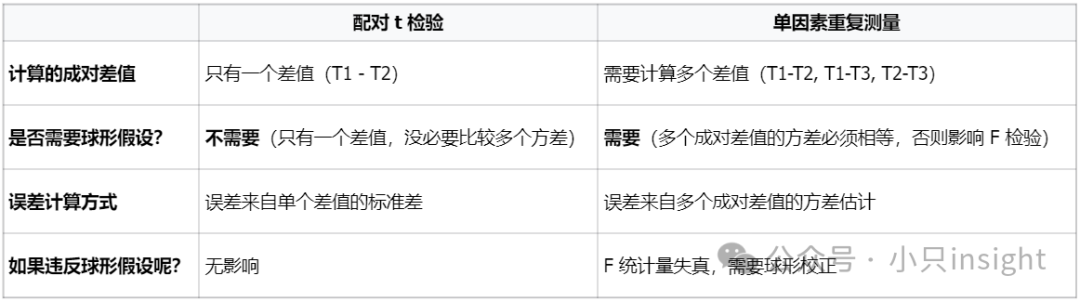
① 当你只分析2个测量点（条件）时，单因素重复测量退化成配对t检验，因为它们的数学推导在这个场景下是一模一样的。

② 但一旦测量点超过2个，配对t检验就不适用了，而可以轻松扩展到任意数量的条件。

那单因素重复测量方差分析能不能分析2个变量？

可以！

虽然大多数统计教材都会说“重复测量ANOVA主要用于3个及以上的条件”，但实际上如果你只有2个条件，ANOVA的结果和配对t检验是完全等价的，P值也一模一样。

不过从习惯上讲，大家还是倾向用配对t检验来做2个变量的分析，毕竟它更简单直接。

不过虽然两者假设基本一致，但单因素重复测量多了一个：

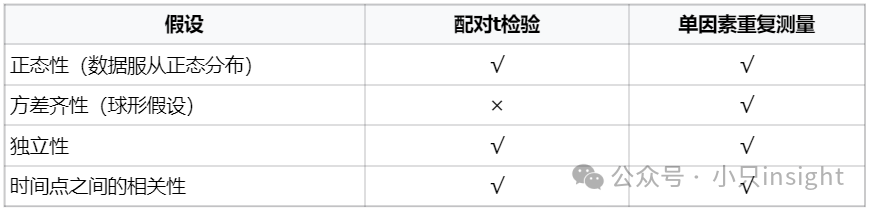
这里最容易忽略的是方差齐性（球形假设），它是ANOVA独有的假设。

什么时候用哪个？

① 2个条件：配对t检验（更简单直接）

② 3个及以上条件：单因素重复测量ANOVA

如果你不想管假设，或者数据本身就偏非正态分布，可以直接用Friedman检验（非参数版重复测量ANOVA）。

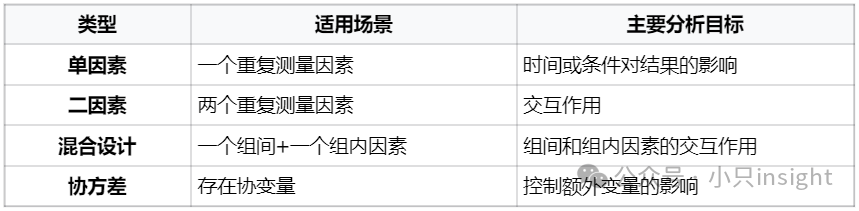
另外拓展一下，跟其他的同门兄弟关系如下：

案例切入

假设我们正在评估1款手机（A）分别在四个维度上进行满意度评分（1-10分）。

研究问题是：

在同一机型下，不同年龄段满意度评分是否存在显著性差异？

SPSS数据录入

在SPSS中，我们需要录入数据，每个被试占据一行，变量名称如下：

按以下步骤设置变量类型：

机型设置为名义变量

满意度评分设置为数值变量

SPSS操作步骤

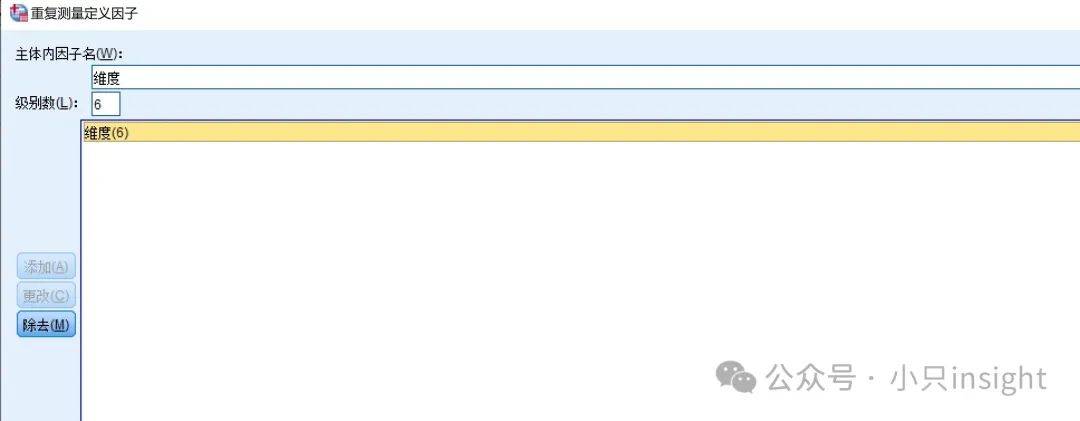
设置重复测量因子

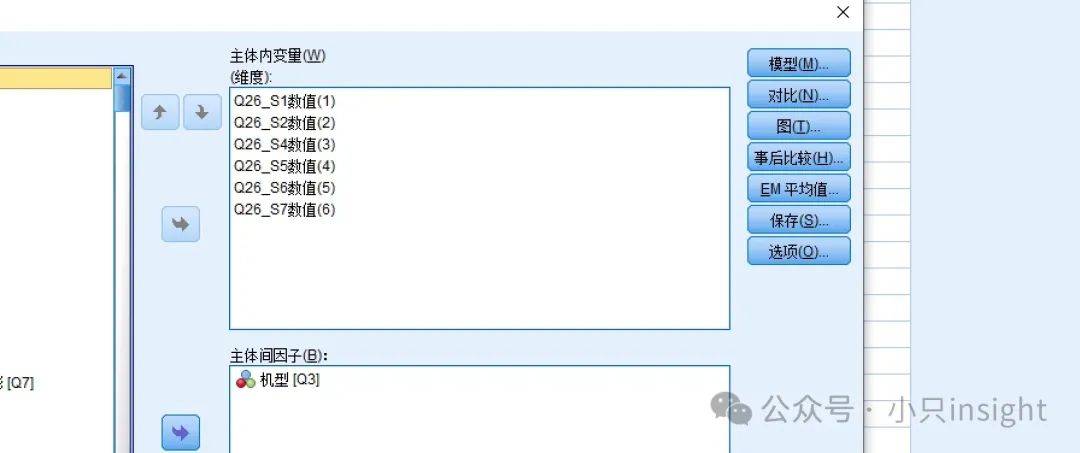
点击分析>一般线性模型>重复测量。

在弹出的对话框中，输入：“维度”。

级别数输入：“6”，点击定义。

一般勾选“描述性统计”、“事后比较”、“效应量估计”。

结果解读

多变量检验

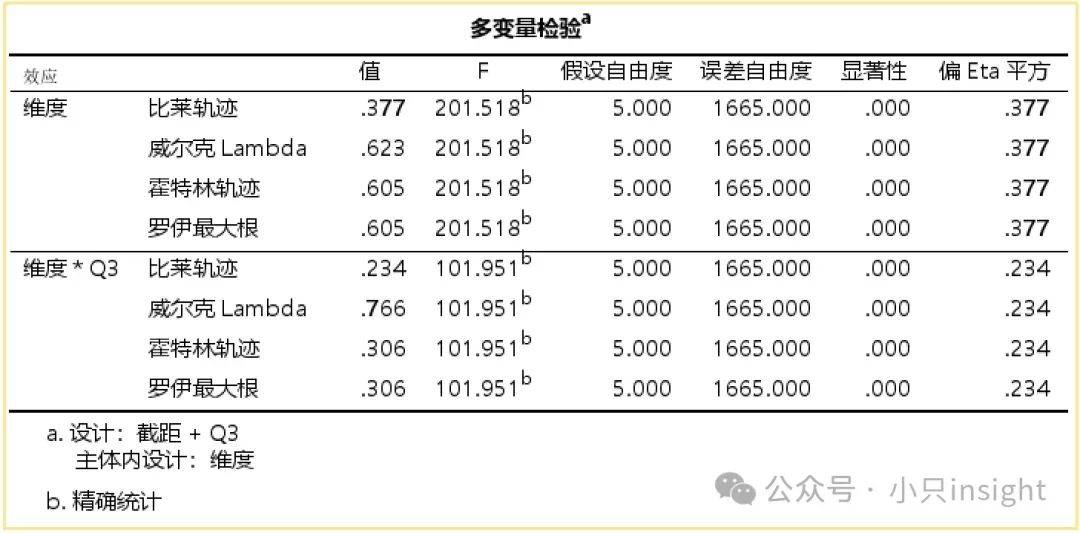
① 所有检验的F值=201.518，p值=0.000，意味着“维度”对因变量的影响极其显著。

② 偏Eta平方=0.377，表示“维度”可以解释37.7%的方差，说明它的影响较大。

③ “维度*Q3交互作用”也显著，但影响力较低：

④ F值=101.951，p值=0.000，依然是高度显著的。

⑤ 偏Eta平方=0.234，说明它解释了23.4%的方差，相比“维度”的37.7%，影响稍弱。

通俗解释：

“维度*Q3交互作用”意味着Q3在某种程度上影响了维度的效果。你研究的是“维度×Q3机型”对满意度的影响，你发现维度仍然是主要因素，但Q3机型在某些情况下会增强或削弱满意度。

拓展：多变量检验是什么？

当你的实验有多个因变量（满意度），而你想同时分析它们受自变量影响的情况时，就需要用多变量方差分析（MANOVA），而不是普通的方差分析。

多变量检验提供了四种统计方法，它们用于评估自变量对因变量的综合影响。

这些计算方式不同，但基本目标都是相同的：看看自变量是否对多个因变量的整体分布有显著影响。

莫奇来球形度检验

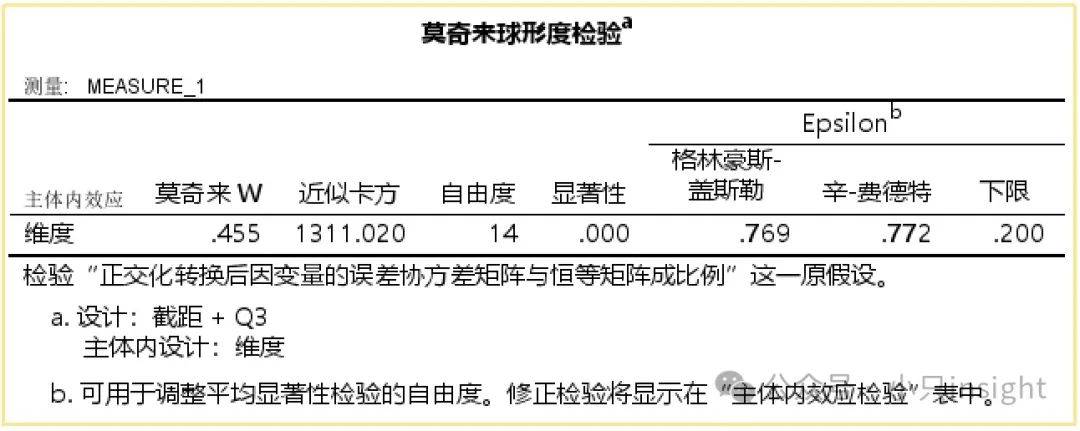
莫奇利W=0.455，远小于1，表明球形假设可能不成立。

显著性p=0.000，小于0.05，因此球形假设被拒绝，意味着不同条件之间的方差并不均匀（数据变化不平稳），不能直接使用标准的ANOVA方法。

由于球形假设被违反，需要修正自由度：

① Greenhouse-Geisser校正因子=0.769

② Huynh-Feldt校正因子=0.772

③ 最小校正下限=0.200（最严格的调整）

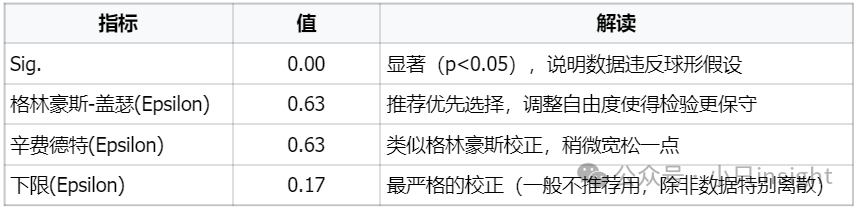
如果Sig.>0.05，说明数据满足球形假设，可以直接使用常规的方差分析结果(假设球形度那一行)。

Greenhouse-Geisser校正是最常用的修正方法，意味着我们在计算ANOVA统计量时，要把自由度缩小到76.9%，以减少第一类错误（误判显著性的概率）。

什么是球形假设？

在重复测量方差分析中，有一个重要的假设：球形假设。

简单来说，就是每个实验条件之间的变化程度要差不多。如果球形假设不满足，就会导致F检验的自由度计算错误，进而影响结果的准确性。

主体内效应检验

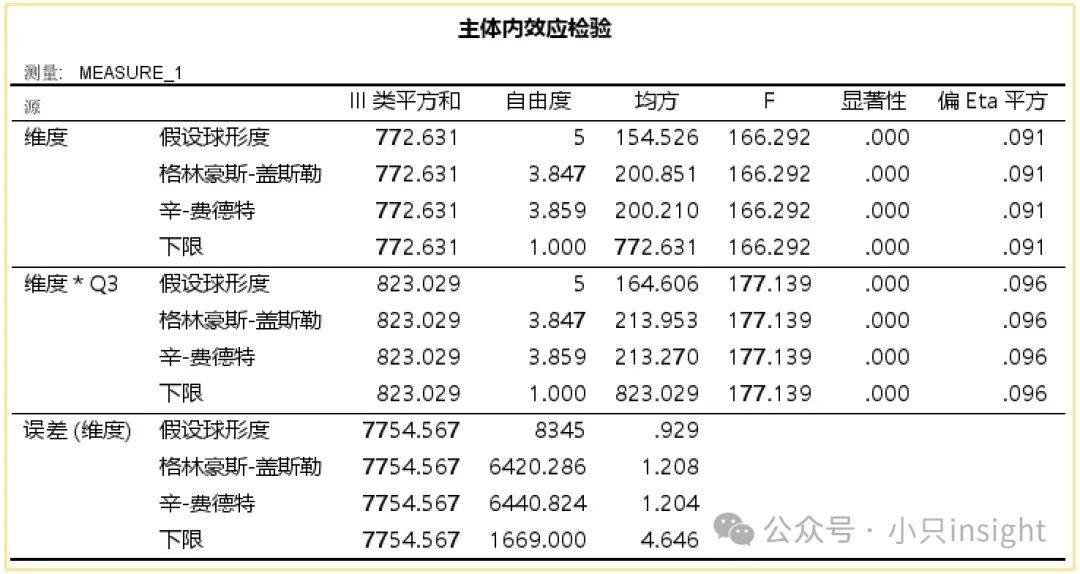
这个表的作用是：

检查“维度”是否对因变量（满意度）有显著影响，同时也检查“维度*Q3交互作用”是否显著。

换句话说，我们想知道：

① 不同“维度”条件下，满意度是否有变化（主效应）。

② Q3是否会影响“维度”对满意度的作用方式（交互作用）。

③ 误差项显示数据的方差和误差程度。

(1)“维度”主效应

F=166.292，p<0.001，偏Eta平方=0.091。

解释：不同“维度”下，满意度发生了显著变化。

偏Eta平方经验标准： 0.01：小效应、0.06：中等效应、0.14：大效应。

这里的 0.091 介于中等和大效应之间，说明“维度”对满意度的影响不小。

(2)“维度*Q3”交互作用

F=177.139，p<0.001，偏Eta平方=0.096。

解释：Q3会影响“维度”对满意度的影响方式。

偏Eta平方：值高于 0.06，但低于 0.14，意味着Q3对“维度”与满意度的关系有较强影响。

(3)误差项

误差的均方（MS）=0.929，意味着在不同被试之间，满意度有一些波动，但整体误差较小，数据稳定。

远大于1，数据有较大噪音，接近1则表示误差较小，数据稳定。

主体内对比检验

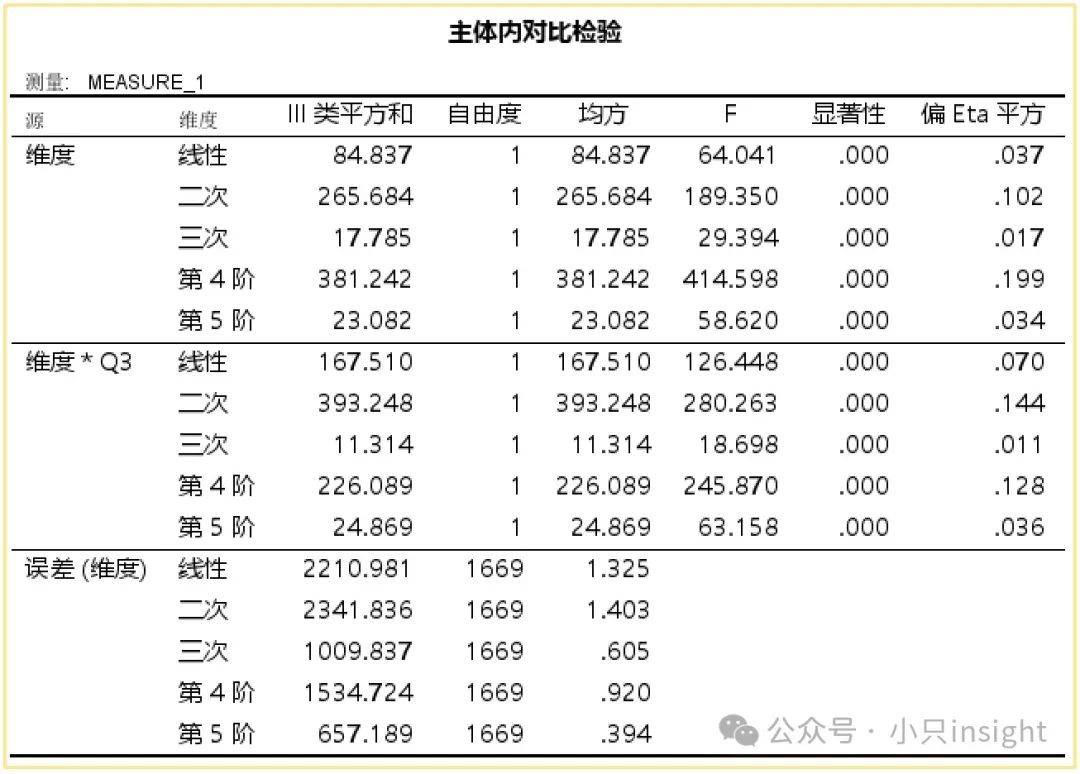
这张表的作用是：分析“维度”对满意度的具体影响方式。

不同于第一张表只告诉我们“维度”有影响，这张表告诉我们“维度”的影响是线性还是非线性。

(1)线性效应

F=64.041,p<0.001,偏Eta平方=0.037

解释：如果“维度”影响满意度呈线性变化（比如随着“维度”增加，满意度逐渐变大或变小）。

(2)二次效应

F=189.350,p<0.001,偏Eta平方=0.102

解释：如果“维度”影响满意度呈U形或倒U形变化，比如满意度在中间维度时最高，但在极端值时下降。

(3)三次及以上效应

说明满意度的变化模式可能不是简单的线性或U形，而是更复杂的多项式模式。

如果“维度*Q3”交互作用在所有阶数上都显著（p<0.001），说明Q3会影响“维度”对满意度的作用方式，并且这个影响可能是复杂的非线性模式，且可能存在交互作用，即某些因素的影响在不同维度下是不同的。

需要做更多的校验分析。

主体间效应检验

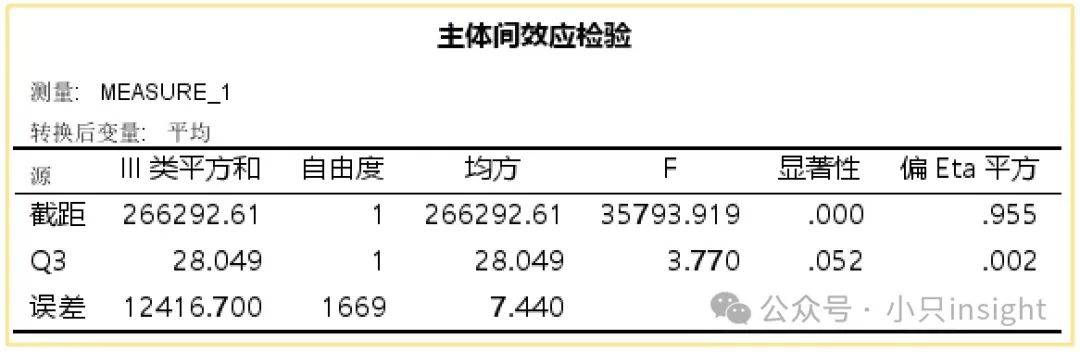
这张表目的是分析不同组别之间的测量变量（满意度）的差异是否显著。

主要关注不同个体群体之间的差异。

操作性话术来讲，这张表检查“截距”和“Q3”是否对因变量（满意度）有显著影响。

截距：代表MEASURE_1(满意度)的整体平均值（没有任何自变量影响时的基准值）。

Q3：这是研究中的一个变量，可能是一个分组变量或一个协变量。这个表告诉你Q3是否影响满意度。

再简单一点来讲，这张表是在问：不同Q3组别的满意度是否有显著差异？

(1)截距

F=35,793.919,p<0.001，偏Eta平方=0.955

解释：截距的p值极小（p<0.001），说明总体均值（满意度的基准值）显著不同于0。

现实意义：这通常没什么特别的意义，除非你关心满意度是否为0。

(2)Q3主效应

F=3.770,p=0.052，偏Eta平方=0.002

解释：p=0.052，略大于0.05，说明Q3对满意度的影响不显著（严格来说）；偏Eta平方=0.002，表示Q3解释了满意度方差的0.2%，影响非常小。

现实意义：这意味着不同Q3组别的满意度差异很小，不足以达到统计学显著水平。

(3)误差项

误差均方=7.440，表示个体之间的变异。

现实意义：误差项告诉我们，个体之间满意度的波动情况。

估算边际平均值(比较主效应)

一句话概括：告诉你不同维度间谁和谁是有显著差异（重中之重)。

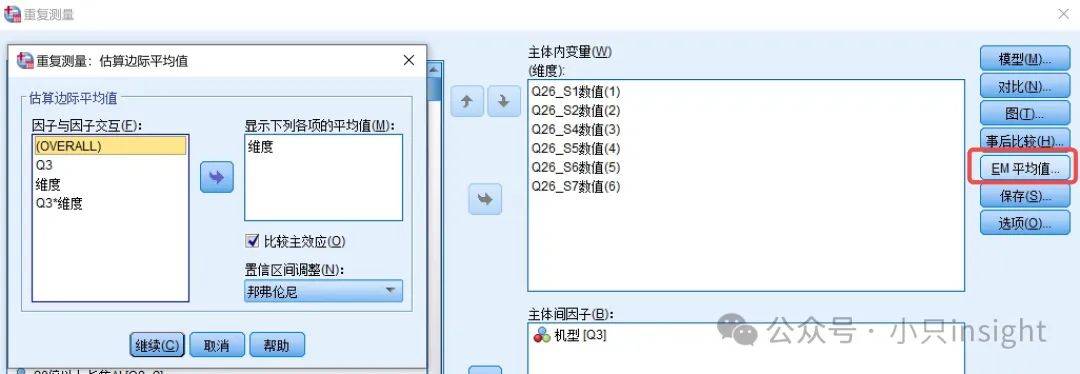
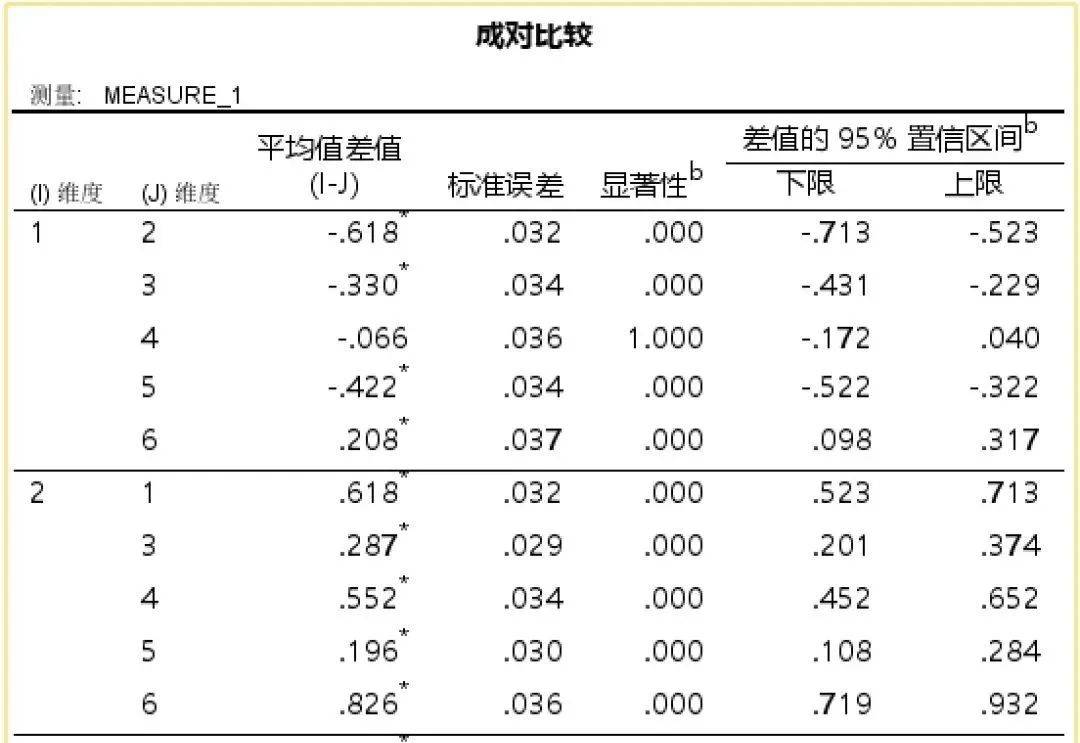
估算边际均值让你看到每个维度的调整均值，但不会直接告诉你显著性。

在选项里勾选比较主效应。

查看“配对比较”表格，寻找显著性（p<0.05）的对比项。

p<0.05表示显著差异，p>0.05表示没有统计学显著差异。

额外说明

在SPSS中进行方差分析时，(4个维度的满意度评价)因变量必须是数值型，否则无法执行分析。

如果你的样本量较小或者评分是等级数据，或者不满足正态分布或球形假设，推荐改用Friedman检验（非参数版本的重复测量方差分析）。

SPSS里面就有该方法。