
用于比较多个独立样本(组)之间的均值是否存在显著性差异。
"单因素":只有一个自变量(因子),例如机型(A、B、C)。
"方差分析":利用数据的方差来判断均值是否有显著差异,而不是直接比较均值。
它解决了多组均值比较的问题。
如果仅有两组数据,我们可以用独立样本t检验。
但当比较三组及以上时,逐个进行t检验会增加第1类错误率。
如果不同组的数据均值不同,那么它们的方差应该较大;如果均值相似,方差则较小。
ANOVA主要计算F统计量来判断是否有显著性差异。
① 计算总方差(SST):所有观测值围绕总均值的离散程度
② 计算组间方差(SSB):各组均值与总均值之间的离散程度
③ 计算组内方差(SSW):每个组内部的数据围绕各自组均值的离散程度
而F统计量用于判断组间差异是否足够大,计算公式为:
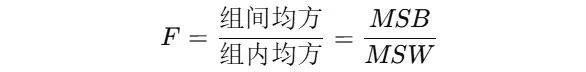
其中:
组间均方(MSB):MSB=SSB/(k−1)
组内均方(MSW):MSW=SSW/(N−k)
判断显著性:
F值越大,说明组间差异越大,相比于组内方差,组间差异更加显著。
计算p值(Sig.),若p<0.05,则拒绝原假设,说明组间均值有显著性差异。
自变量:一个分类变量,且至少有两个水平(如手机型号)。
因变量:一个连续变量(如满意度)。
核心问题:自变量的各个水平是否对因变量产生显著差异?
正态性:各组数据需近似服从正态分布。
方差齐性:各组的方差需大致相等。
独立性:不同组别的观测值相互独立,无配对或重复测量关系。
我们邀请90名用户,每位用户只测试其中一款相机,然后给出1-10分的满意度评分。

变量说明:
因变量:满意度评分(1-10分)
自变量:相机机型(A、B、C)
目标:检验三种机型的评分是否有显著性差异。
运行单因素方差分析
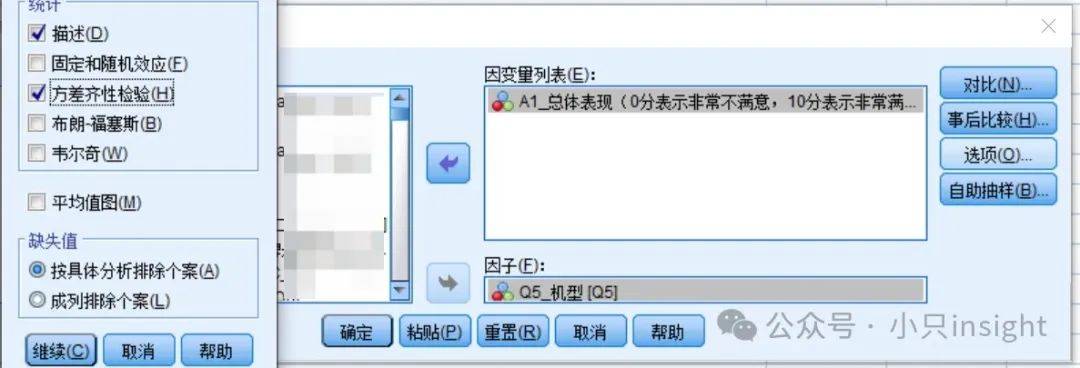
路径:Analyze(分析)→CompareMeans(比较均值)→单因素方差分析
设置变量:
DependentList(因变量)→选择“满意度评分”
Factor(自变量)→选择“机型”
勾选以下选项:
Descriptivestatistics(描述性统计)
Homogeneityofvariancetest(方差齐性检验)
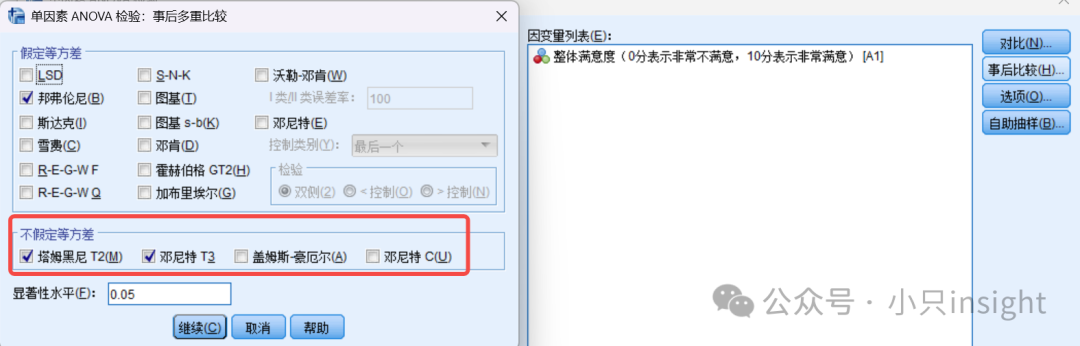
PostHoc(事后检验)(选择Bonferroni或其他)
点击OK运行分析。
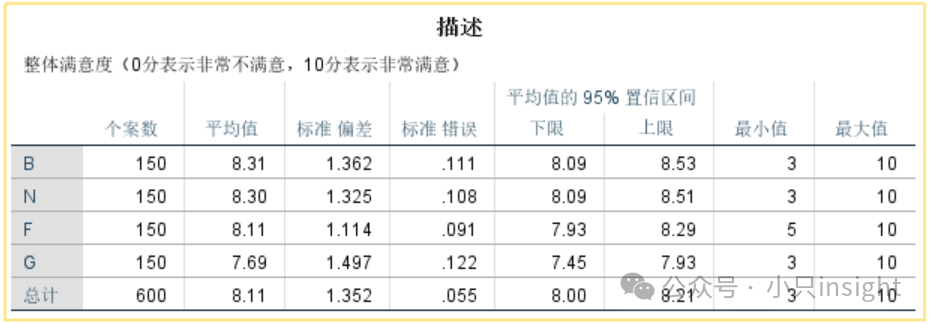
这一部分展示了不同机型(B、N、F、G)的整体满意度评分的均值、标准偏差、标准误、置信区间(95%)、最小值和最大值。
如何解读?(仅作示例)
满意度均值:B、N、F的满意度接近(8.31、8.30、8.11)。
标准偏差:G机型的标准偏差最大(1.497),说明其满意度评分分布较为分散,用户的评价较不一致。
置信区间:例如,B机型的满意度均值是8.31,我们可以95%确信它的真实均值落在8.09到8.53之间。
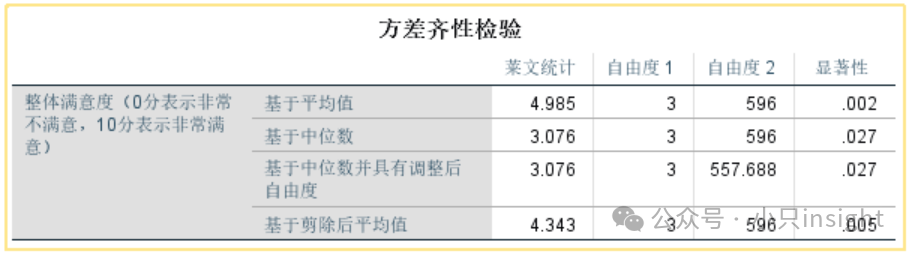
方差齐性检验的目的是检查不同组别的方差是否相等,这是进行方差分析的前提假设。
如果 p 值 > 0.05,表示没有显著差异,说明方差是齐的(满足方差分析的前提)。
如果 p 值 < 0.05,表示方差有显著差异,说明方差是不齐的(不满足方差分析的前提)。
如何解读?
方差齐性检验的p值为0.002(<0.05),说明不同机型的满意度评分的方差存在显著差异,即数据的方差不齐。
由于方差不齐,我们在进行ANOVA之后需要谨慎解读结果,甚至可以考虑Welch’sANOVA或非参数检验来进一步验证。
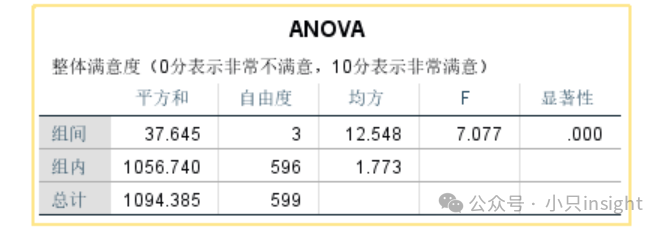
方差分析用于检验不同机型的满意度均值是否存在显著差异。
如何解读?
F值=7.077,p值=0.000(远小于0.05),说明不同机型的满意度均值存在显著差异。
但是,ANOVA只能告诉我们「至少有一个机型的满意度均值与其他不同」,但不能告诉我们具体哪些机型之间有显著差异。
因此,我们需要进一步进行事后检验。
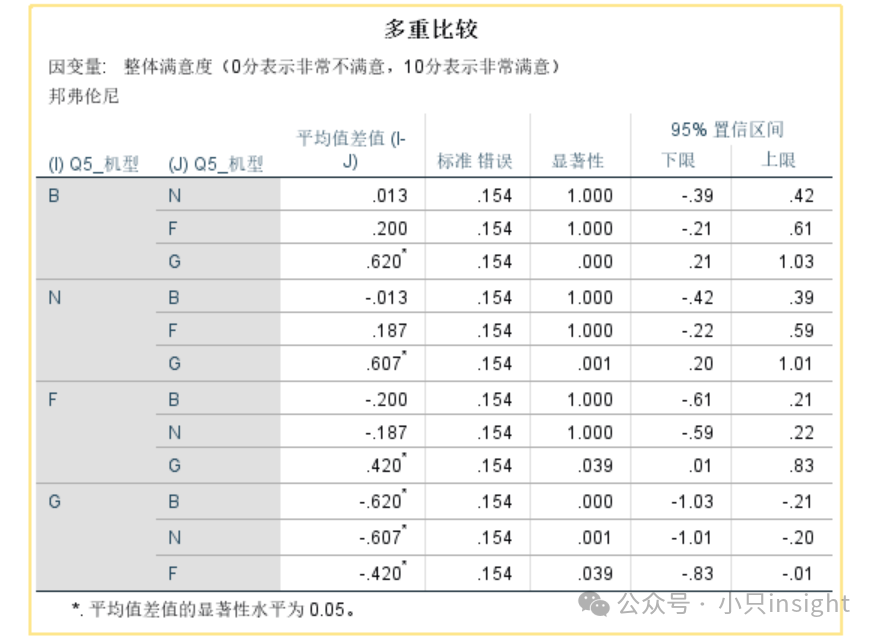
事后检验用于进一步分析不同机型之间的均值差异是否显著。
带*的表示显著性水平<0.05,说明该组之间存在显著差异。
如何解读?
B、N、F之间的差异不显著(p>0.05),说明这些机型的满意度均值在统计上没有显著不同。
B-G、N-G、F-G之间的差异显著(p<0.05),说明G机型的满意度显著低于其他机型。
B机型的满意度比G高0.620,p=0.000,显著。
N机型的满意度比G高0.607,p=0.001,显著。
F机型的满意度比G高0.420,p=0.039,显著。
整体来看,不同机型的满意度评分确实存在显著差异(p=0.000)。
B、N、F机型满意度无显著区别(p>0.05),但G机型满意度显著低于其他机型(p<0.05)。
我们看到目前的数据检验其实是方差不齐(p = 0.002)的,真实情况下应该怎么办?
① 继续使用 ANOVA,但注意解释
如果样本量相等(目前数据中每组 n = 150),ANOVA对方差不齐的鲁棒性较强,误差不会太大。
所以可以继续使用ANOVA,但要谨慎解读结果,尤其是p值接近 0.05 时。
② 采用 Welch’s ANOVA
Welch’s ANOVA是普通ANOVA的改进版,它允许方差不齐时使用,会调整自由度,使得显著性检验更可靠。 如果你希望更严谨的分析,可以重新计算Welch’s ANOVA,看看 p 值是否仍然显著。
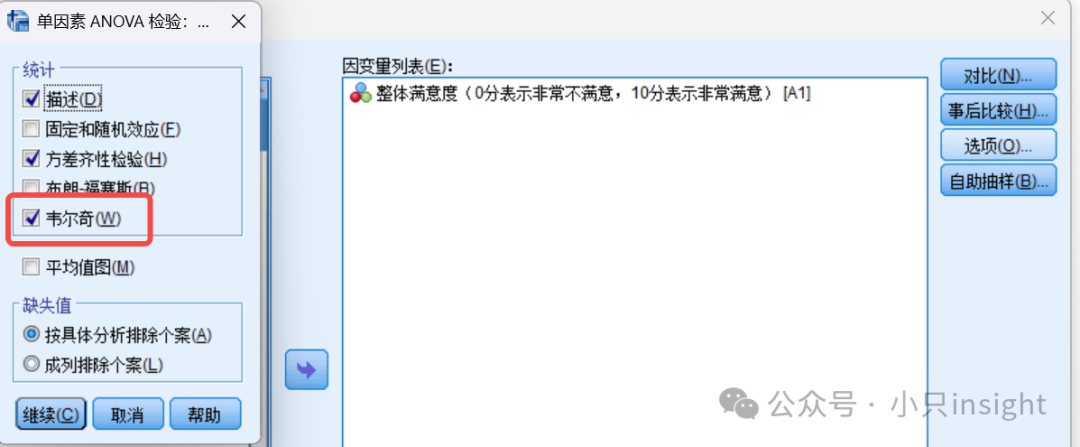
点击 “选项 (Options)” 按钮,然后勾选 “均等方差未假定的稳健检验 (Welch)”。
其他步骤一致
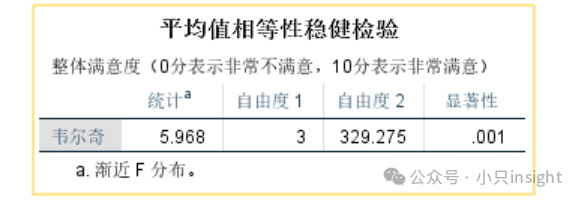
Welch统计量:用于检验均值是否存在显著差异。
p = 0.000(小于 0.05),说明不同机型满意度均值有显著差异,结论依然稳健。
可以继续进行事后检验(如以下红框内方法)。
第1类错误也叫α错误,是指:
当原假设H0其实是真实的,但我们误拒绝了它,即:
其实A、B、C机型的用户满意度是相同的,但我们错误地认为它们不同。
通常,我们设定显著性水平α=0.05,表示:
在一次统计检验,有5%的概率会犯第一类错误,即原本没有差异,但我们误判为有差异。
假设我们要比较三款相机(A、B、C)的满意度评分:
A vs B(第1次t检验)
A vs C(第2次t检验)
B vs C(第3次t检验)
如果每次t检验的α=0.05,则:
进行1次t检验,错误率=5%
进行2次t检验,错误率≈9.75%
进行3次t检验,错误率≈14.26%
每次t检验独立进行,每次有5%的可能性出现假阳性(错误发现显著性)。
当我们进行多次检验时,每1次都有可能犯错,而这些错误的概率是累积的。
而单因素方差分析只做1次总检验,而不是多个独立t检验,所以整体第1类错误率仍然保持在5%。
只有当ANOVA检验结果有显著差异,才进一步进行事后检验,严格控制第1类错误率。
想象一个赌场的游戏:
你掷一次骰子,如果掷出“6”,你就输(相当于犯第1类错误率)。
你掷一次骰子的概率是 1/6 = 16.7%,如果只掷一次,输的概率不高。
但如果你连续掷 3 次呢?至少出现一次“6”的概率就会远远高于 16.7%。
每多掷一次骰子,你输的概率(犯错的概率)都会变大。
这跟多个 t 检验的第1类错误率累积原理是一样的。
组内方差,大家应该都好理解,组间方差呢?
用一个例子来简单说明:

总体均值:
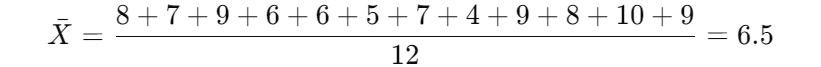
组间平方和(SS_B):
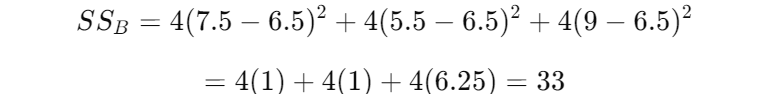
组间自由度(df_B):
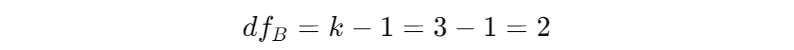
组间方差(MS_B):
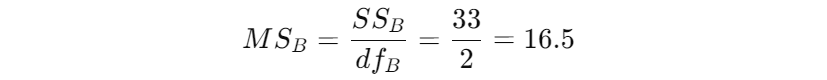
以上。