
上一轮提到线性回归,这次要提到它的好朋友“逻辑回归”(Logistic Regression)。
在市场和用户研究领域,逻辑回归是一个非常重要的统计工具。
它不仅能够帮助我们理解变量之间的关系,还能为预测决策提供数据支持。

可以想象,逻辑回归像是在预测一扇门的开关。门打开(事件发生)与关闭(事件不发生)之间并不是一个简单的“是”或“否”,而是通过几个因素的影响(比如天气、心情、时间等)来判断概率。
逻辑回归的任务就是找到这些因素与门开关之间的关系。
用一句话说清楚与线性回归的关系:逻辑回归=线性回归+sigmoid函数。

用直白的话来讲
逻辑回归是一种用于分类问题的回归分析方法,主要用于预测二元(0或1)结果。
它的目标是通过自变量(特征)来估计因变量的概率。
比如,预测某个用户是否会购买某项产品(购买=1,不购买=0)。
用数理的话来讲
逻辑回归利用逻辑函数(sigmoid函数)将线性回归的输出映射到0和1之间。
其核心在于如何将线性组合的结果转换为概率值。
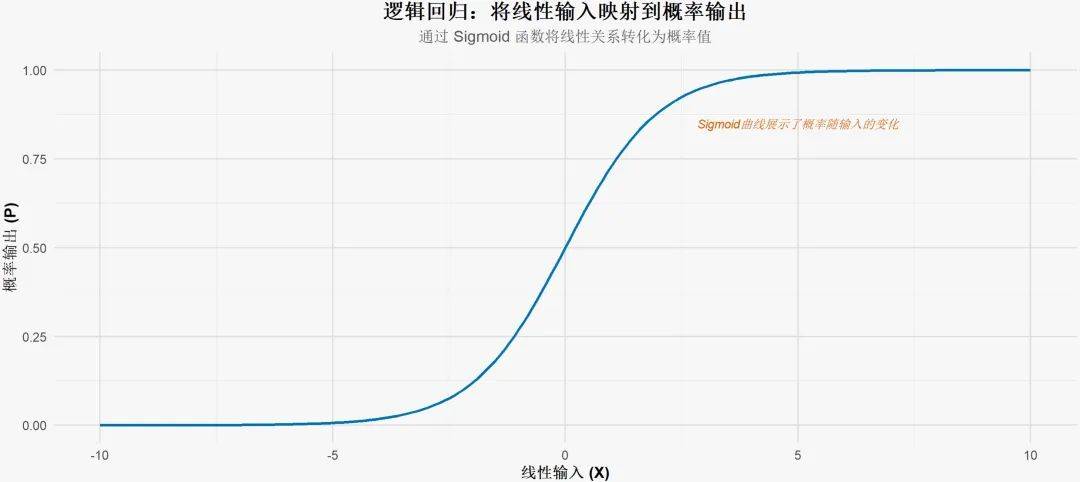
前述提到,逻辑回归使用了一个叫做“Sigmoid函数”的曲线,将线性回归的输出转化成了概率的形式。
可以一步步来看看它是怎么做到的。
假设我们有一个输入变量 X,目标是预测它属于不同类别的概率。
如果用线性回归的话,模型的预测结果可以表示为:
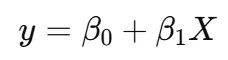
y是对因变量的预测值。虽然看上去很直观,但问题是“线性回归的输出是没有限制的”。
例如,当 X 变大或变小时,y 会增大或减小,理论上可以达到任何数值。
而概率的值只能在0到1之间,因为概率不能超过100%或者低于0%。
为了解决这个问题,逻辑回归引入了一个S形的曲线函数,也就是逻辑函数,它的公式为:

这里的 e 是自然对数的底(大约是2.718),而 β0 + β1*X 是线性回归的输出。逻辑函数将线性回归的输出 “拉回” 到 0 和 1 之间。
逻辑函数的输出随着 X 的变化是非线性的,它会生成一个S形曲线,如下图所示:

中间区域:当 β0 + β1 X 接近于0时,事件发生的概率是50%。
左右两侧的平缓区域:当 β0 + β1 X 变大时,此时P(y=1|X) ≈1 。相反,当 β0 + β1 X 变得非常小(负数很大)时,P(y=1|X) ≈0。
过渡平滑:S形曲线的优势在于其“平滑过渡”效果,这让概率随着 X 的变化平滑调整,而不是突然跳跃。

4. 逻辑回归的决策边界
在二分类问题中,我们通常会设定一个阈值(比如0.5),来判断事件是否会发生。
根据逻辑回归模型输出的概率:
当 P(y=1|X) ≥ 0.5,我们预测类别为1。
当 P(y=1|X) <0.5,我们预测类别为0。
这里只对最为主流的分类做展开,其余的可以自行查阅。
定义
二项逻辑回归是最基础的逻辑回归模型,适用于仅有两种可能结果的分类问题。
应用场景
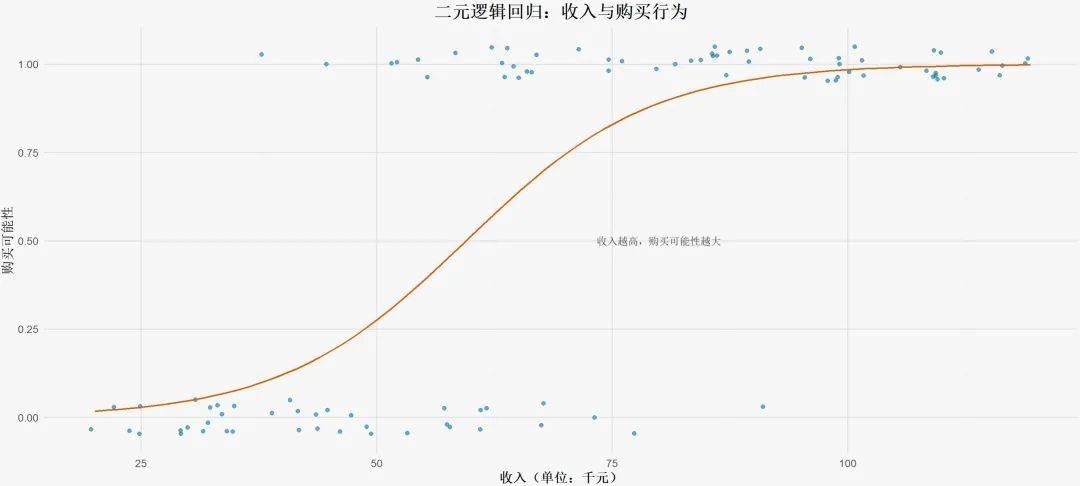
在用户研究领域中,二项逻辑回归常用于二元行为预测,例如用户的某种购买决策、某类服务的选择等。
例如,用户是否会购买产品(购买/不购买),或个体是否患有某种疾病(患病/不患病)。
定义
多项逻辑回归是对二项逻辑回归的推广,用于有多个类别的因变量。
多项逻辑回归适用于无序分类问题,即不同类别之间没有天然的顺序关系。
应用场景
用户研究中,常用于预测用户对不同产品类别的偏好或选择,如选择A产品、B产品或C产品。

定义
序数逻辑回归用于有序多分类情况,即因变量的不同类别具有天然的顺序关系。
该模型在二分类和多项逻辑回归的基础上引入了“序”的概念。
它有一项重要假设是比例优势假设(Proportional Odds Assumption),即假设自变量对不同类别间的转换具有相同的影响,即每个类别的对数几率之间的回归系数是相同的。
应用场景
在用户研究中,可以用序数逻辑回归预测用户对产品的满意度(如“非常满意”、“满意”、“一般”、“不满意”)。

① 因变量的二分类或多分类性质
因变量(也称目标变量、响应变量)应是二分类或多分类的离散变量。
② 自变量之间的线性关系
逻辑回归假设自变量(预测变量、解释变量)之间的关系是线性的,即模型假定因变量的对数几率(log-odds)与自变量呈线性关系。这是广义线性模型中的一项核心假设。
自变量和因变量之间并不要求严格的线性关系,但要求自变量的线性组合与logit函数(对数几率)之间存在线性关系。
③ 自变量的独立性
自变量之间应尽量不存在多重共线性,否则会导致模型参数不稳定,标准误偏大,显著性检验失效等问题。
检查自变量的多重共线性可以通过计算方差膨胀因子(VIF)来实现。
④ 样本独立性
逻辑回归假设样本之间是相互独立的,即每个观测值都是相互独立的,且不依赖于其他观测值。
若数据存在时间序列性或组间相关性,则需进行额外的调整或选择其他适合的模型。
⑤ 类别的独立性(针对多项逻辑回归)
对于多分类的逻辑回归,存在一个重要的假设,即类别的独立性(Independence of Irrelevant Alternatives, IIA)。IIA假设要求一个类别的选择与其他类别的相对选择无关。
IIA假设是指:某一类的选择概率与其他类的相对比率应当是固定的,即一个新类别的加入或移除不会影响原有类别之间的相对比率。
⑥ 样本量要求
逻辑回归对样本量的要求较高,尤其是在分类不平衡的情况下。样本量不足会导致模型在预测类别时不稳定或过拟合。
一般建议每个类别至少有10倍于自变量数目的样本量,以保证模型的估计稳健性。
① 数据敏感性
逻辑回归对异常值和缺失值较为敏感,可能影响模型的预测准确性。
② 多类分类
对于多类分类,逻辑回归的性能可能不如其他复杂模型(如决策树、随机森林等)。
① 决策树
决策树是一种非参数的分类方法,能够处理复杂的非线性关系,适合更复杂的决策场景。
② 随机森林
随机森林通过集成多棵决策树的结果,提高预测精度,适用于大数据集和高维特征。
假设某电商平台希望预测用户是否会购买某款新产品。通过调查数据,我们得到了用户的性别、年龄、浏览历史等特征。
步骤:
收集1000名用户数据,构建逻辑回归模型。
自变量:性别(0=女性,1=男性)、年龄、浏览次数。
因变量:购买(0=未购买,1=已购买)。
结果:
模型预测准确率为85%,其中年龄和浏览次数对购买概率影响显著。
银行希望通过逻辑回归模型评估贷款申请者的信用风险。主要自变量包括收入、负债率、信用历史等。
步骤:
收集2000名申请者的数据。
自变量:收入、负债率、信用卡使用率。
因变量:违约(0=未违约,1=违约)。
结果:
模型发现,负债率是影响违约概率的关键因素。
至于具体在SPSS等软件中的操作实现,各位可自行探索,对于常规的上文提到的逻辑回归方法,SPSS中均有涉及,操作以及解读均上手简单。