卡方检验：万能差异检验工具

文/小只

卡方检验，市场及用户研究领域中，极其常用的工具。

什么是卡方检验？

卡方检验是一种用于检验两个分类变量之间独立性的非参数统计检验方法。

它通过比较观测频数和理论频数来判断实际观察到的分布与期望的分布之间是否有显著差异。

前提条件

① 样本独立性：数据应当是独立的，即每个观测值应来自不同的个体或样本。

② 分类数据：卡方检验用于处理分类数据（名义数据或序列数据）。

② 样本容量：每个单元格的期望频数应足够大。

一般来说，卡方检验的一个常见规则是每个单元格的期望频数应该至少为5。如果有些单元格的期望频数小于5，可以考虑合并类别或使用Fisher精确检验（对于小样本）。

更精细的如下：

适用于四格表应用条件：

(1) 所有的理论数 T≥5 并且总样本量 n≥40，用 Pearson卡方进行检验。

(2) 如果理论数 T＜5 但 T≥1，并且 n≥40，用连续性校正的卡方进行检验。

(3) 如果有理论数 T＜1 或 n＜40，则用Fisher’s 检验。

R×C表卡方检验应用条件：

(1) R×C表中理论数小于5的格子不能超过1/5。

(2) 不能有小于1的理论数；不满足 (1) 或 (2) 时，均采用 Fisher’s 检验。

如果实验中有不符合R×C表的卡方检验，可以通过增加样本数、列合并来实现。

实现步骤

① 准备数据

收集数据并将其整理成列联表。

列联表是一种用于展示两个分类变量频数的表格，是卡方检验的基础。

② 计算期望频数

在卡方检验中，期望频数是基于列联表的行总计和列总计计算得出的，计算公式略。

③ 计算卡方统计量

将所有单元格的观测频数和期望频数代入卡方检验公式，计算卡方统计量。

④ 确定自由度和临界值

根据列联表的行数和列数，计算自由度，并查阅卡方分布表找到相应的临界值。

⑤ 做出决策

将计算出的卡方统计量与卡方分布表中的临界值进行比较。

如果卡方统计量大于临界值，则拒绝原假设，认为变量之间存在显著关联；否则，接受原假设。

局限性

① 样本大小的影响

卡方检验对样本大小较为敏感。样本量过小可能导致检验的统计效能不足，而样本量过大则可能放大微小的差异，使得结果具有统计显著性但缺乏实际意义。

② 适用于分类数据

卡方检验仅适用于分类数据（如名义变量或有序变量），而不适用于连续变量。

③ 期望频数的要求

卡方检验要求每个单元格的期望频数应至少为5。

卡方检验类型

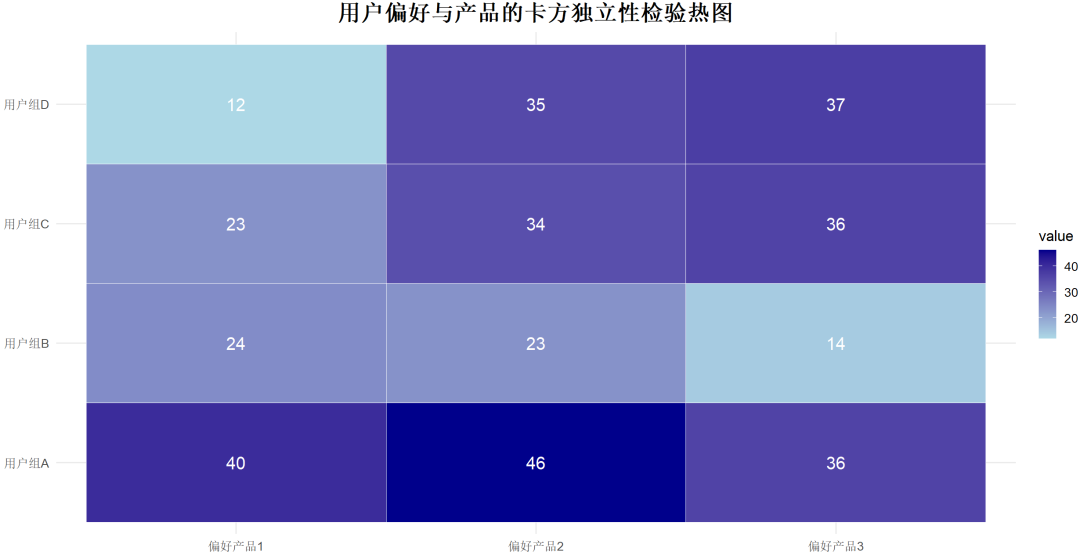
卡方独立性检验

理解：卡方独立性检验用于评估两个分类变量之间是否存在统计学上的关联。

该检验通过构建一个二维的列联表来计算各个类别的期望频数，并与实际观察频数进行比较。

“卡方独立性检验”就是我们平时常用的“卡方检验”。

适用前提条件：

① 所有的期望频数都不应该低于1。

② 至少80%的期望频数应该大于或等于5。

变量类型：分类变量

示例：分析消费者的购买行为与人口统计学特征（如性别、年龄）之间的关系。例如，评估性别和购买特定品牌产品之间是否存在显著关联。

说明：

为什么我们常说的“卡方检验”被称为“卡方独立性检验”？

虽然使用卡方检验主要是为了检验不同组别之间的差异，但这些差异是在更广泛的统计意义上作为“分类变量之间的关联”来评估的。

无论从“关联”角度还是从“差异”角度去理解，卡方独立性检验在本质上都是在探讨两个分类变量之间的关系。当我们说“差异”时，实际上是在具体化这种关系，即在分类变量的不同组别之间是否存在显著的不同。

在日常研究和分析中，人们通常更关心实际意义上的差异，这就是为什么卡方独立性检验常常被用于差异分析。这并不改变检验的本质，只是反映了人们关注点的不同。

卡方同质性检验

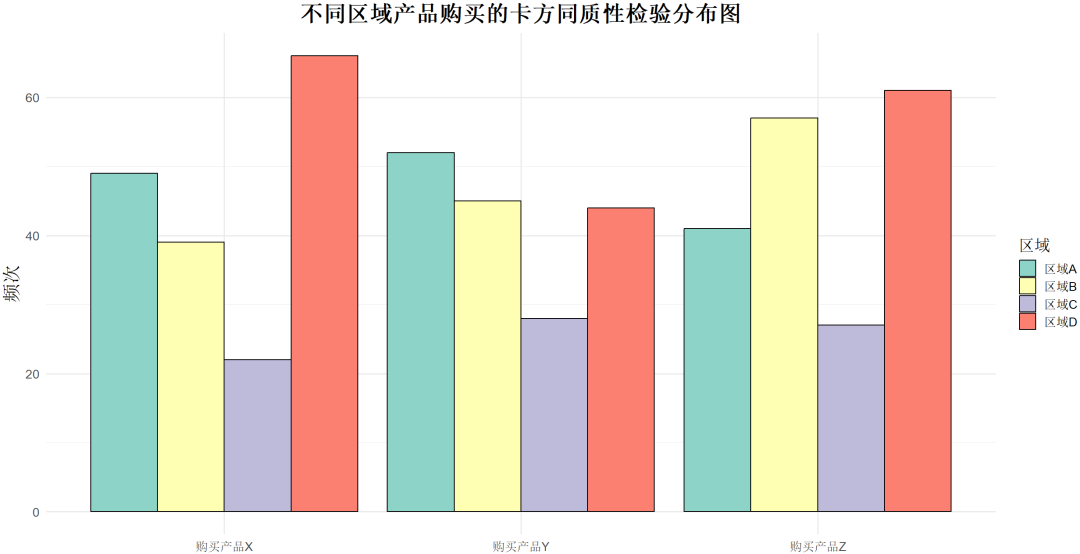
(拓展了解为主)

理解：用于判断多个群体在某一特定属性的分布上表现是否相同。

卡方独立性检验用于探究两个分类变量是否在单一群体中相互关联。

适用前提条件：

① 数据是分类的。

② 每个单元格的期望频数应不小于5。

变量类型：分类变量

示例：假设你在研究不同城市的顾客对某一产品的购买偏好。你有三个城市的数据，每个城市的数据都显示顾客是否购买该产品。你可以使用卡方同质性检验来检验这三个城市的顾客购买偏好分布是否一致。

说明：

从统计学角度看，卡方独立性检验和卡方同质性检验在技术上非常相似，甚至可以认为它们在计算上是等价。

它们都基于比较实际观察到的频数分布与期望频数分布的差异。

因此如果你对相同的数据应用这两种检验，计算出的卡方统计量和p值应该是相同的。

在SPSS中，独立性检验和同质性检验都可通过交叉表功能实现。

卡方拟合优度检验

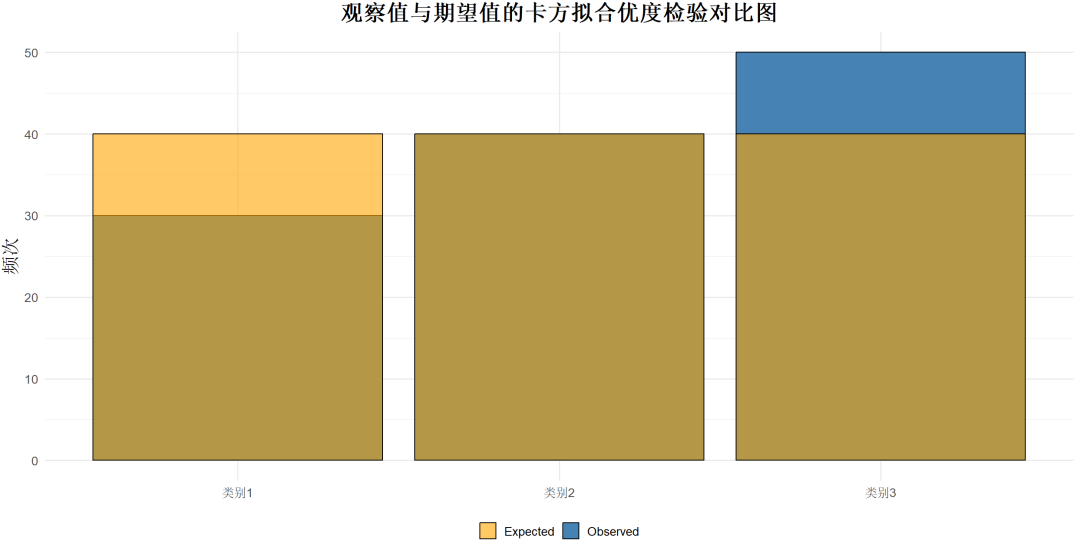
理解：用于检验一个分类变量的观测分布是否与一个特定的理论分布相符合。

该方法特别适用于单一分类变量的分析(经典如分析某一群体的多选题比例)。

适用前提条件：

① 每个类别的期望频数不应少于5个。

② 期望频数必须依据一个合理的理论或模型进行计算，如均匀分布、正态分布等。

③ 需要使用绝对频数而不是相对频数(其他方法也一样)。

④ 数据之间不存在相关性或重复性，应相互独立。

变量类型：分类变量

示例：验证消费者在不同品牌之间的选择是否符合市场份额的预期分布。

配对卡方检验(McNemar's Test)

理解：配对卡方检验是独立性检验的一种变体，专门用于分析在同一组样本上测量的两个分类变量。

它特别适合于处理前后测设计或配对样本设计的研究。

适用前提条件：

① 数据必须是配对的：处理来自同一组受试者的两次观测。

② 数据必须是二分类，每个观测值只能属于两个可能的类别之一。

③ 要求数据能够整理成一个2x2的配对表格。

变量类型：分类变量

示例：分析广告前后用户对某品牌的选择是否显著变化。

Cochran检验 (Cochran's Q Test)

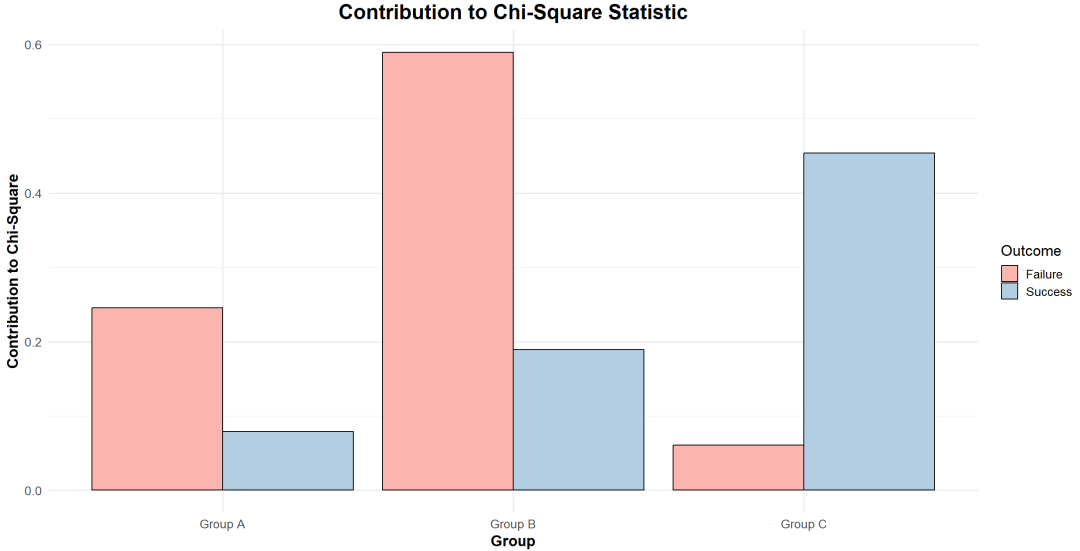
理解：非参数检验，用于分析三个或更多配对样本之间的二分类变量的差异。

该检验是McNemar检验的扩展版，适用于处理多个相关样本的情况。

适用前提条件：

① 数据必须是配对的：即样本必须来自同一组受试者或单位，且每个受试者在多个条件下都被测量。

② 数据必须是二分类的：即每个观测值只能属于两个可能的类别之一（例如“成功/失败”等）。

③ 样本数量固定：每个受试者在每个条件下的观测都必须是独立的。

变量类型：分类变量

示例：某公司想了解消费者对三种不同品牌的广告的偏好，以优化广告策略。这三种品牌分别为品牌A、品牌B和品牌C。为了了解消费者的偏好，让消费者在观看后选择自己更喜欢的广告类型。

实际应用

① 调查问卷中的偏好分析

假设我们想要分析不同年龄段消费者对某款新产品的喜好。我们可以使用卡方检验来判断年龄与产品偏好之间是否存在显著关联。

数据形式可能如下：

② 用户行为数据中的模式识别

例如，研究人员可能希望了解用户在不同平台上的行为模式是否一致，或不同用户群体之间的行为是否存在显著差异。

数据形式可能如下：