CxHub客户体验社区-用户研究、体验爱好者学习交流社区，专注客户体验(CX)研究。
社交媒体
文/小只
在市场研究中，数据往往不是严格符合正态分布。例如，用户满意度评分、消费者偏好等变量通常呈现出偏态分布，或者数据中存在离群值，这时传统的t检验、方差分析等参数检验方法可能无法满足分析的要求。
而非参数检验无需依赖数据的具体分布假设，通常基于数据的秩（Rank）来进行比较，因而具有较好的鲁棒性。
秩和检验 (Rank-Sum Test)正是非参数检验中的一种典型方法。
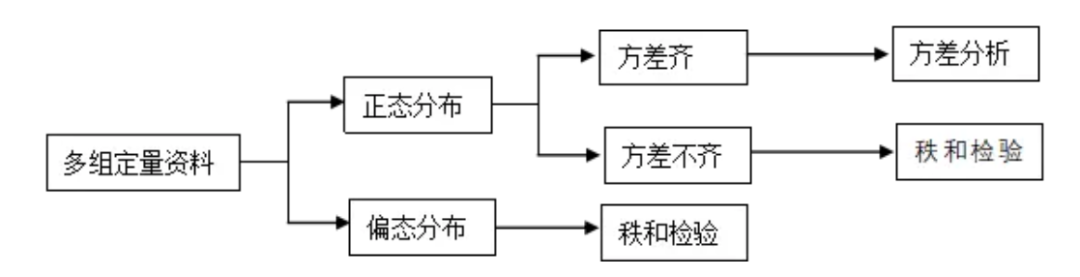
先将所有样本数据按照大小排序，再根据排序后的位次（即秩）来比较不同组之间的总体差异，而不是直接比较原始数据的大小。
这种方法尤其适合处理不满足正态分布的数据，以及数据含有明显离群点的情况。
秩分配：将所有观测值按照从小到大的顺序排列，并赋予相应秩（最小值为1，依次递增）。
秩和计算：分别计算每个组的秩和。
检验统计量：通过计算各组的秩和差异，结合检验统计量来判断这种差异是否具有显著性。
不受数据分布影响
秩和检验无需假设数据符合正态分布，适用于各种类型的分布数据。
处理离群值
相比参数检验方法，秩和检验对离群值不敏感，结果更为稳健。
灵活性高
能够应用于不同类型的数据，适用于多种研究场景。
由于秩和检验只考虑数据的秩信息，忽略了数据的具体值，因此可能会丢失部分信息。
Mann-Whitney U 检验(也称 Wilcoxon 秩和检验)
理解：非参数统计方法，比较两组独立样本的差异情况。
不需要假设数据的正态分布。
适用前提条件：
样本来自相同分布且样本大小可以不相等。
两组样本相互独立，彼此之间无关联。
不要求数据服从正态分布，适用于非正态分布的数据。
采用秩次而非原始数据进行检验。
变量类型：连续变量或有序分类变量。
示例：比较男性和女性对某一新产品的满意度评分，判断两者之间是否存在显著差异。
局限性：
仅比较秩次信息，可能会丢失数据的绝对差异信息。
当样本大小差异较大时，检验的功效可能降低。
对于含有大量重复值的数据，检验的准确性可能受到影响。
Wilcoxon 符号秩和检验(Wilcoxon Signed-Rank Test)
理解：非参数统计检验方法，比较两组配对样本的差异情况。
它常用于评估在某种干预或处理前后，同一组对象的变化情况。
适用前提条件：
配对样本数据成对出现，每对数据独立。
需要对每对样本的差值进行检验，不要求差值服从正态分布。
适用于数据量较小的情况，不要求大样本量。
变量类型：连续变量或有序分类变量。
示例：比较同一批消费者在使用新旧两个版本的移动应用程序后的满意度评分，判断两个版本之间是否存在显著差异。
理解：用于检验三组或更多独立样本的差异情况。
是单因素方差分析的非参数替代方法。
适用前提条件：
样本来自相同分布且样本数量可以不同。
各组样本相互独立。
不要求数据服从正态分布，适用于非正态分布的数据。
适用于组别数量超过两组的情境。
变量类型：连续变量或有序分类变量。
示例：比较不同年龄段消费者对某一品牌的偏好评分，判断年龄段之间是否存在显著差异。
理解：用于检验三组或更多配对样本的差异情况。
是重复测量方差分析的非参数替代方法。
适用前提条件：
样本数据成对出现，每对数据独立。
不同条件下的分布形态应当是相似的。
不要求数据符合正态分布。
变量类型：连续变量或有序分类变量。
示例：比较同一批用户在使用不同品牌智能手机后的满意度评分，判断品牌之间是否存在显著差异。
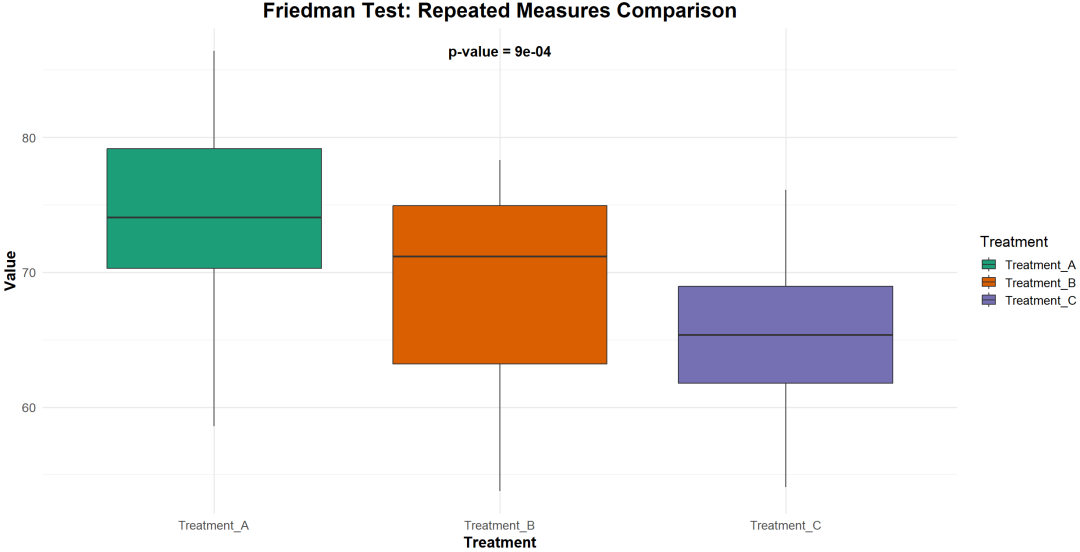
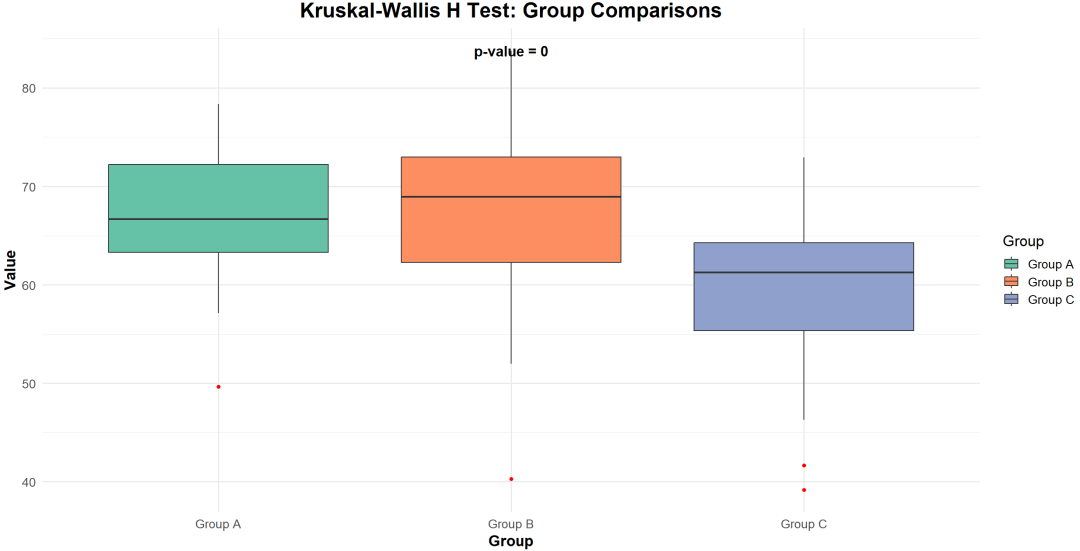
某公司推出了一款新型智能手表，目标群体为不同年龄段的消费者。公司进行了市场调查，收集了来自三个不同年龄段的用户对手表的满意度评分（分别为18-25岁，26-35岁，36-45岁）。由于评分数据不符合正态分布，因此决定使用Kruskal-Wallis H检验来比较三个年龄段用户的满意度评分是否存在显著差异。
步骤一：数据收集收集了各个年龄段用户的满意度评分，并整理成表格：
用户组别 | 满意度评分 |
18-25岁 | 5, 6, 7, 8 |
26-35岁 | 4, 6, 7, 9 |
36-45岁 | 3, 5, 7, 8 |
步骤二：秩分配将所有用户的满意度评分合并，按大小排序，并为每个评分分配相应的秩。
用户组别 | 满意度评分 | 秩 |
36-45岁 | 3 | 1 |
26-35岁 | 4 | 2 |
36-45岁 | 5 | 3.5 |
18-25岁 | 5 | 3.5 |
26-35岁 | 6 | 5.5 |
18-25岁 | 6 | 5.5 |
18-25岁 | 7 | 7.5 |
26-35岁 | 7 | 7.5 |
36-45岁 | 7 | 7.5 |
18-25岁 | 8 | 10 |
36-45岁 | 8 | 10 |
26-35岁 | 9 | 12 |
步骤三：秩和计算计算每个年龄段用户的秩和值：
18-25岁：3.5 + 5.5 + 7.5 + 10 = 26.5
26-35岁：2 + 5.5 + 7.5 + 12 = 27
36-45岁：1 + 3.5 + 7.5 + 10 = 22
步骤四：计算检验统计量H根据各组的秩和值和样本量计算检验统计量H：
H = (12 / (N * (N+1))) * Σ (Rᵢ² / nᵢ) - 3 * (N+1)
其中，N为总样本量，nᵢ为每组的样本量，Rᵢ为每组的秩和。
步骤五：判断显著性根据计算出的H值，查找相应的卡方分布表，确定显著性水平（p值）。如果p值小于预设的显著性水平（如0.05），则可以认为不同年龄段用户的满意度评分存在显著差异。
