CxHub客户体验社区-用户研究、体验爱好者学习交流社区，专注客户体验(CX)研究。
社交媒体
K-Medoids是一种基于中心的聚类算法，是K-Means的“兄弟”，又称Partitioning Around Medoids，简称PAM。
"Partitioning Around Medoids" 可以翻译成“围绕中心点的划分”或“基于质心的分区”。“Medoids”是指每个聚类类别中最典型或最具代表性的对象。
Medoids必须是原始数据集中真实存在的对象，类似于K-means算法中的中心点（centroid），但不像K-means那样计算出的平均值。
PAM算法通过迭代调整每个聚类的Medoids以及将数据点重新分配到最近的Medoid所属聚类中。
这对于异常值更加鲁棒，因为它不受单个远离中心点的数据点的影响。
鲁棒：常用于描述统计模型或算法对于数据中的离群值、噪声或偏差的抵抗能力。鲁棒的统计方法能够在数据存在异常时仍能提供可靠的结果。
意味着K-Medoids能够更好应对非凸形状的数据分布和含有异常值的情况，因为它使用的中心总是数据集中真实的数据点。
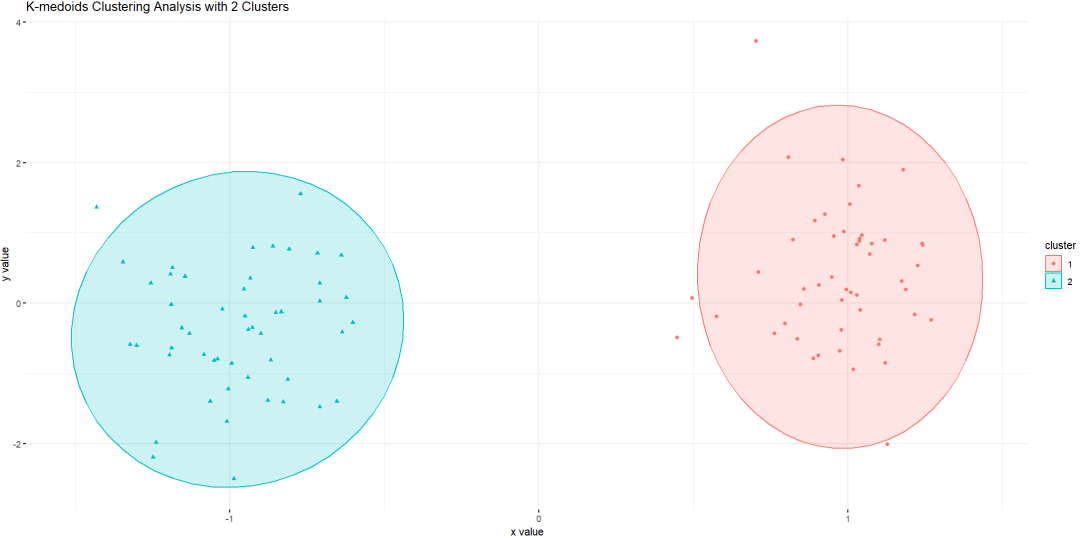
① 选择初始中心点：从数据集中随机选择K个对象作为初始中心点。
② 计算距离：计算每个对象与中心点的距离，将其分配到最近中心点所在的簇。
③ 更新中心点：对于每个簇，计算簇内所有对象的平均距离，选择距离最小的对象作为新中心点。
④ 重复步骤2与3，直至满足停止条件（如中心点变化小于设定阈值或达到最大迭代次数）。
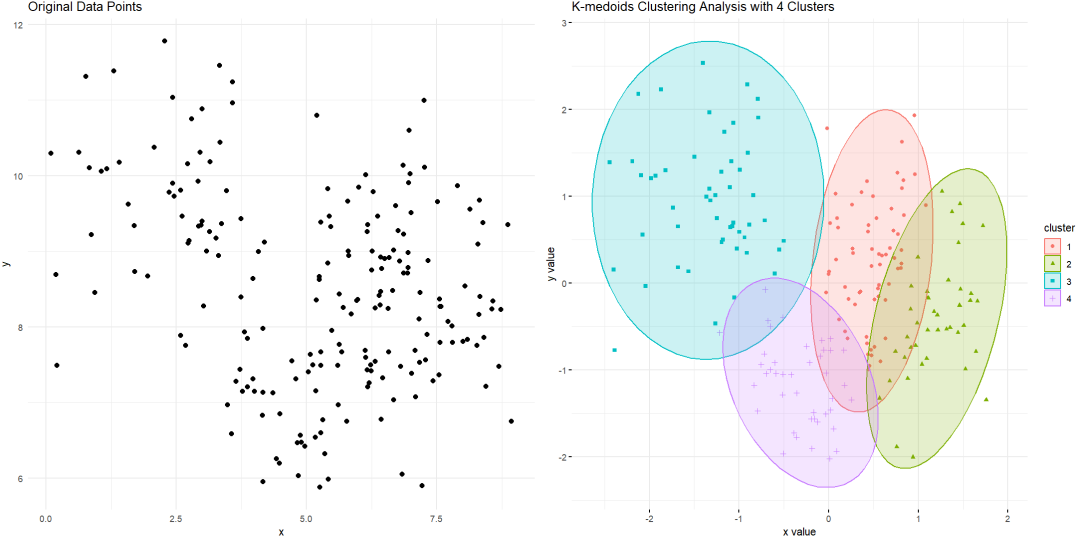
① 确定聚类数量k：需要预先设定聚类的数目k，可以通过肘部法则、领域知识等方法来确定。
详见《聚类分析如何“科学”确定聚类数？》
② 数据集准备：数据预处理，包括数据清洗、缺失值处理、标准化或归一化等。
③ 数据可量化：K-Medoids适用于数值型或类别型数据（经过编码），且数据集应该足够大。
④ 针对凸型数据：更适合于球形or凸形状的簇，因为是基于距离度量来计算簇之间的相似性。
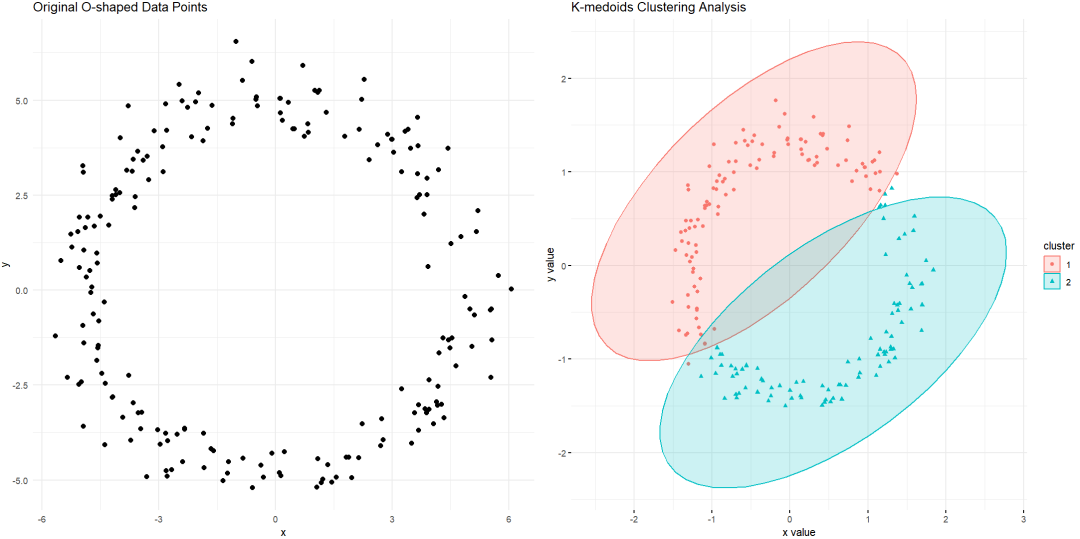
① 抗异常值干扰：由于选取的是实际数据点作为中心，因此对异常值不敏感。
② 分布适应性强：对于不规则形状的集群，K-Medoids较K-Means有更好的聚类效果。
③ 直观易解释：聚类中心是真实存在的数据点，便于理解和可视化。
① 对初始化敏感：如果初始的medoids选择不当，可能会陷入局部最优解。
② 计算成本较高：K-Medoids比K-Means算法更为复杂，尤其当数据规模增大时，计算效率较低。
实现K-Medoids聚类的软件工具有R、Python。
R：可以使用cluster包中的pam函数实现。
Python：可以使用pyclustering库进行。
以R语言实现为例。
在R中，K-Medoids聚类算法的具体实现通常是通过pam()函数来完成，它会采用相同初始中心点和迭代停止条件，或使用了固定随机种子以确保结果的可重复性。
因此，如果在R中多次运行K-Medoids聚类算法，使用相同的初始条件和停止条件，通常情况下会得到相似or相同的结果。
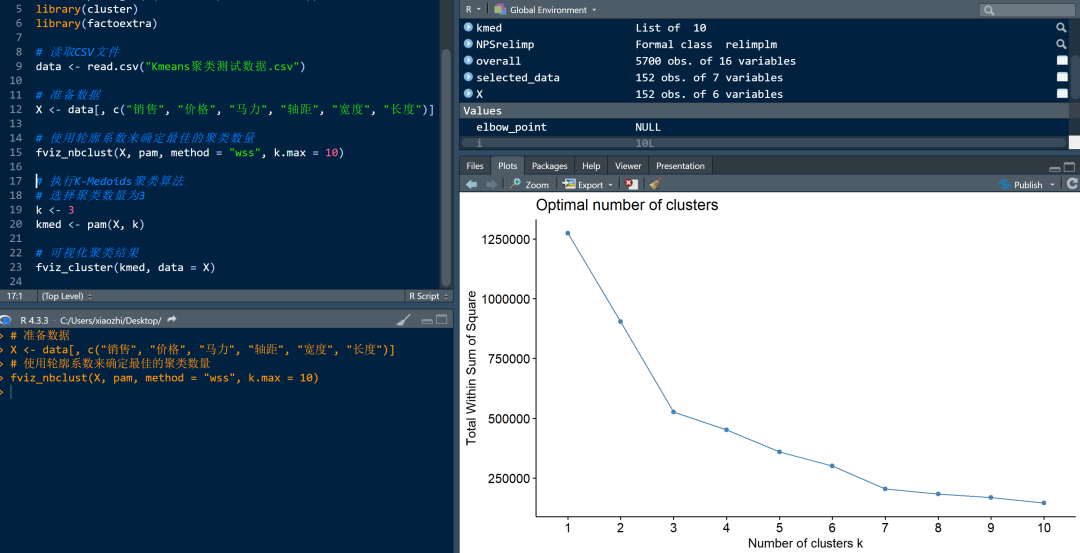
样本被划分仅仅是研究工作的开始，需要把每个样本的聚类标签导出（生成一个新的文档），后续再进行相应的分析工作。
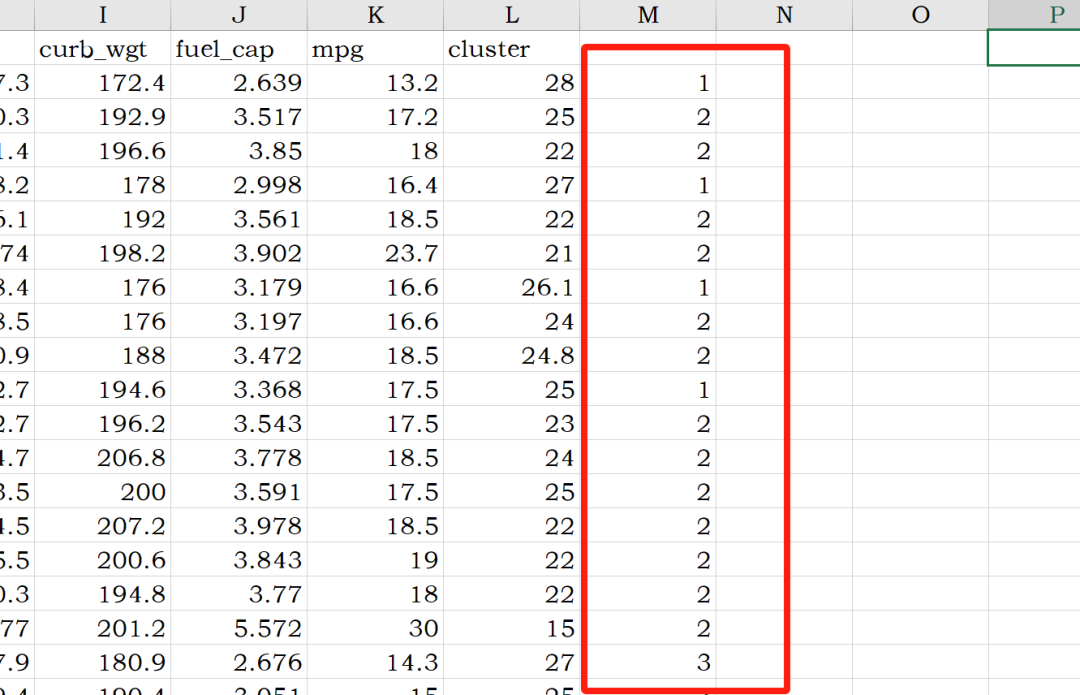
由于初始中心点是随机选取的，采用默认的聚类算法包实现的聚类结果存在偶然偏差性，为提升聚类效果，可尝试以下方法：
① 使用不同的初始中心点初始化算法，可尝试多次运行以迭代到最好的结果（最常用方法）。
② 调整迭代停止条件，例如增加迭代次数或设置更严格的收敛条件。
③ 改变聚类数量，观察不同数量下的聚类效果。
④ 更换其他不依赖于初始状态选取的聚类算法，如DBSCAN 聚类等。
以方法1作为示例
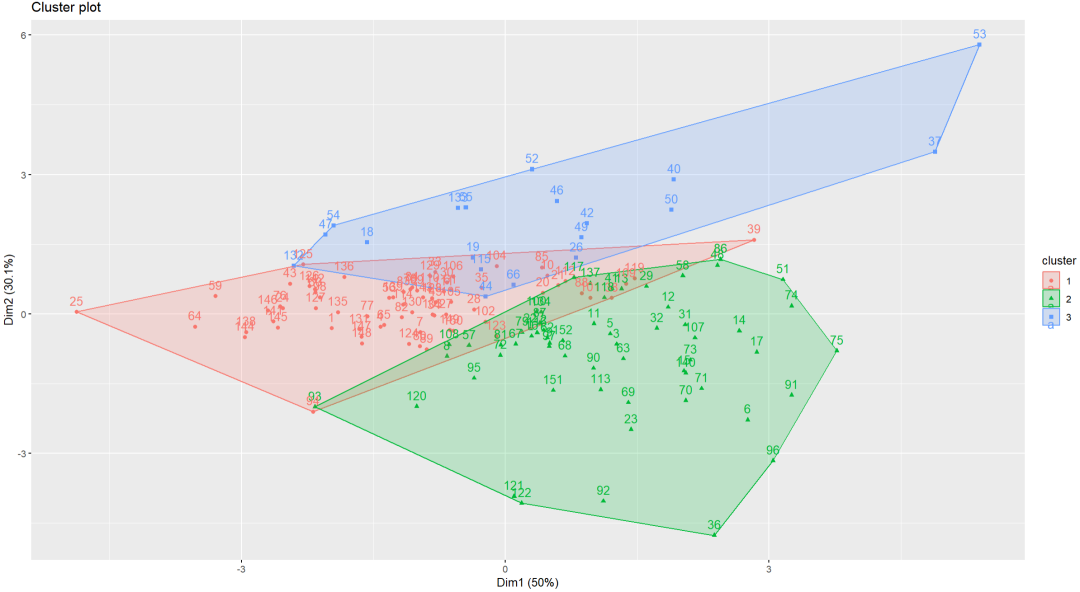
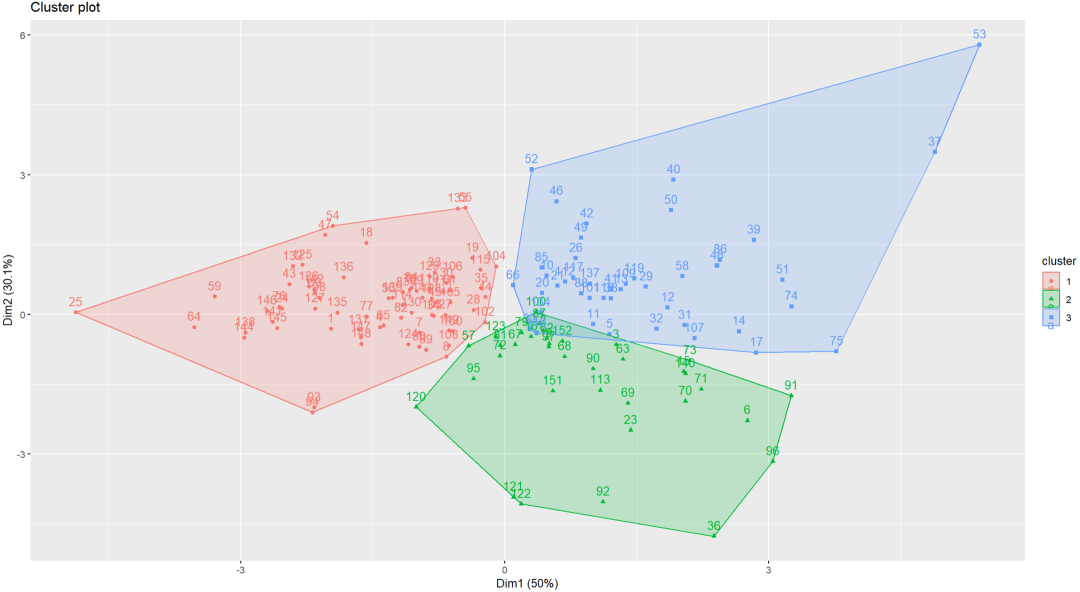
这段代码使用了pam()函数执行K-Medoids聚类算法。其中，参数k表示要分成的簇的数量，这里设置为3；参数nstart表示随机选择初始中心点的次数，这里设置为20。
在每次迭代中，pam()函数会随机选择不同的初始中心点，然后根据这些初始中心点进行聚类分析。通过多次迭代，可以得到多个不同的聚类结果。
在所有20次运行结束后，pam()函数会根据SSE（误差平方和）在所有运行中找到的最佳聚类结果，即数据点到其medoid的距离之和最小的聚类。
最后，这段代码会返回一个包含最佳聚类结果的对象kmed。
① 客户细分：最核心的应用场景。通过对客户数据进行聚类，识别不同的客户群体，进而进行策略制定。
② 市场趋势预测：通过对市场数据的聚类分析，发现市场中的潜在趋势和机会。
③ 其他的与大部分的聚类算法类似，不再一一描述。
稍微提一下K-medians算法(每个簇中心点是其成员数据点在每个维度上的中位数)，这种方法同样减少异常值的影响。但这种方法已经在K-means聚类的文章中有所提及，整体上三者原理类似，就不在后续文章中单独赘述。
END
