
因子分析是指研究从变量群中提取共性因子的统计技术,最早由英国心理学家C.E.斯皮尔曼提出。
简单而言,对于n个原始变量Y1......YP来说,那些高度相关的变量很可能会遵循一个共同的潜在结构:可称之为公共因子 (Common factor)
通过探索变量之间的相关系数矩阵,根据变量的相关性大小对变量进行分组,使同组内变量间的相关性较高,不同组变量的相关性较低。
这些“公共因子”一般难以直接观察可得,故又称为潜变量 (latent variables)。这在心理学、社会学及行为科学等学科中非常常见,比如“情商”、“智力”、“社会阶层”、“性别认知”等。
在科学研究&商业调查中,我们往往希望尽可能多地收集反映研究对象的多个变量,但变量的增加会导致数据采集以及分析的难度增加,在大多数情况下许多变量之间可能存在相关性,意味着那些表面看上去不一样的变量可能往往只是“一个硬币的两面”——从不同的侧面反映同一个维度的信息。
这时候需要对数据进行“降维”处理——在尽可能不损失或者少损失原始数据信息的情况下,将原始的多个变量和指标变成较少的几个综合变量,而各综合变量之间彼此是不相关的,这种变量被称为公共因子。
在市场调研领域,这些因子等同于定量问卷调研中的李克特量表评分指标,多个指标所组成的集合就是“公共因子”,而多个指标的得分所组成的集合就是“公共因子得分”。
R型因子分析:从原始变量出发,基于变量的相关系数矩阵进行求解
Q型因子分析:从原始样本出发,基于样本的相关系数矩阵进行求解
大白话来讲:R型因子分析就是列为变量,行为样本;Q型因子分析就是列为样本,行为变量。
但目前暂时没有Q型因子分析的典型运用场景,一般我们说因子分析, 默认就是R型因子分析。
探索性因子分析(EFA) :顾名思义“探索”,即在没有任何前提预设假定下,反复探索,聚合出最适公共因子。
一般在市场调研领域运用较广,操作难度也较低,SPSS即可实现。
验证性因子分析(CFA):顾名思义“验证”,即已经有前提预设假定下,检验先前提出的因子结构的适合性。
这种方法应用于理论框架(成熟量表)的检验,尤其是心理测量领域,一般用AMOS软件实现。
没有异常值: 前期进行数据清洗,通过多种方法检验异常样本or离群值(具体方法不做展开);
数值型/连续型变量: 因子分析的变量要求为数值型变量(比例型数据也可以,0-1二分变量为可视作特殊的连续型变量);
足够样本量: 样本数必须大于变量数,最少50组样本,理想状态样本数最好为量表题项数的5倍及以上,若不能满足5倍及以上的要求,最低样本数也需在150组以上;
例外情况:如果做综合评价分析,一般要求样本量多于指标数即可,如基于多个维度来对全国各城市进行综合打分,样本量无须作严格要求;
具备相关性,但无完美多重共线性: 通过KMO(Kaiser-Meyer-Olkin)和巴特利特球形检验(Bartlett Test of Sphericity) or 反映像相关矩阵检验(Anti-image correlation matrix)检验相关性(少用,不做展开);
(如无兴趣,以下部分可忽略)
KMO检验:用于考察变量间的偏相关性,取值0~1之间,当所有向量间的简单相关系数平方和远远大于偏相关系数平方和时,KMO统计量越接近1,变量间的偏相关性越强,因子分析效果越好。一般统计量在0.8以上为适应做因子分析,<0.5则不适宜做因子分析。
该检验是对原始变量之间的简单相关系数和偏相关系数的相对大小进行检验
Bartlett球形检验:以变量的相关系数矩阵为出发点的。它的零假设是相关系数矩阵是一个单位阵,即相关系数矩阵对角线上的所有元素都是1,所有非对角线上的元素都为零。即检验各个变量是否各自独立,若P<0.05,不服从球形检验,应拒绝各变量独立的假设,即变量间有较强相关;P>0.05时,服从球形检验,各变量相互独立,无法提取公因子,不能做因子分析。
具体涉及到因子分析的其它概念,通过SPSS软件操作过程中进行解释梳理。

但这里有那么多的设置项,怎么选?
傻瓜式操作如下:
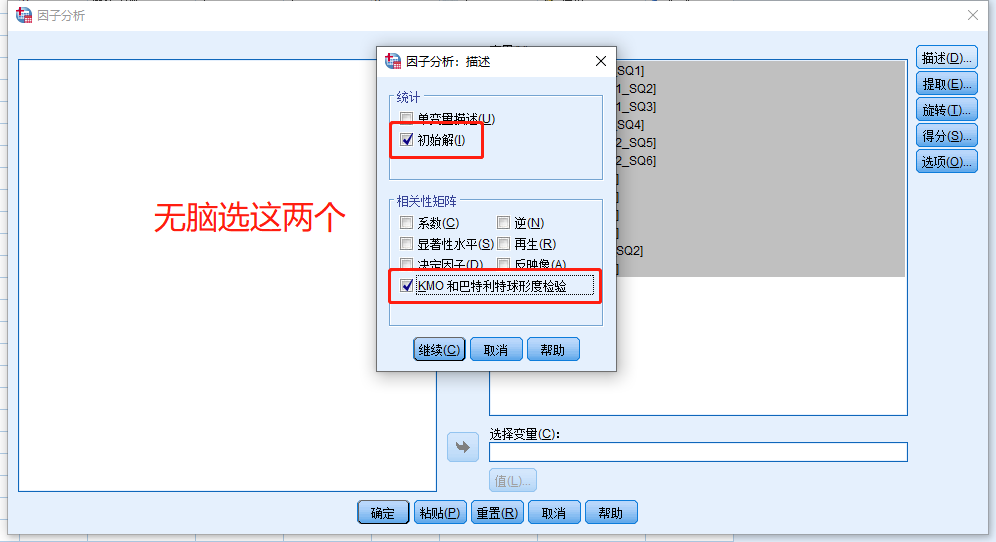
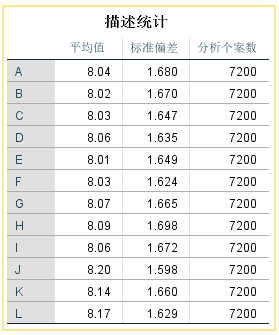
单变量描述:得到各个变量的平均值、标准偏差、分析个案数的表格
一般不需要选
初始解:得到各个变量的初始公因子方差
一般是默认会选
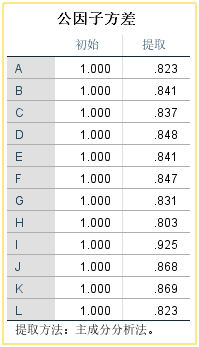
公因子方差(变量共同度) :每一个变量能多大程度上被公因子所“表达”,“表达”得越好,“提取”的值越大,一般大于0.5即可以说是可以被表达,但更通常会要求>0.7才会比较稳健。
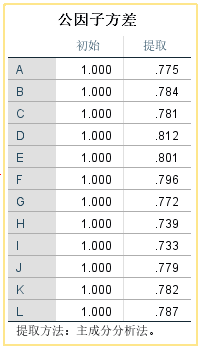
本例中A的公因子方差为0.775,说明几个公因子能够解释A的方差的77.5%;
相关性矩阵:主要计算各个变量之间的相关性
至于用到什么相关性矩阵检验的方法工具,SPSS中均有呈现,但一般我们均选用KMO和巴特利特球形检验的方法进行检验(其他方法可自行搜索)。
若KMO和巴特利特球形检验结果显示Sig.<0.05(即p值<0.05)时,说明各变量间具有相关性,因子分析有效。
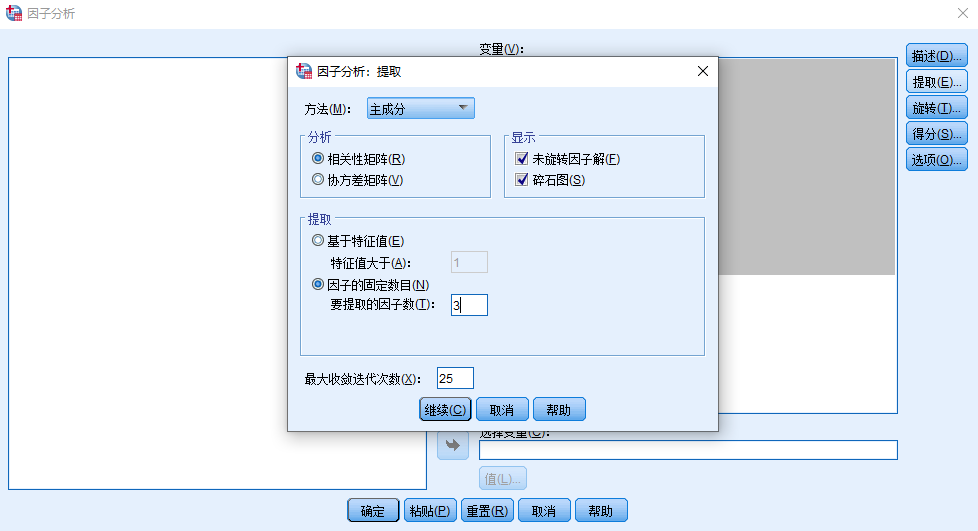
方法:95%都是默认选择【主成分分析】,其他方法如最大似然法等应用较少
主成份方法不是做主成分分析,而是一种提取公因子的方法,不要弄混了
分析:【相关性矩阵】(不要选择协方差矩阵,否则后续结果不好分析)
显示:【未旋转的因子解】:输出未经过旋转的因子载荷矩阵,一般没有参考价值。
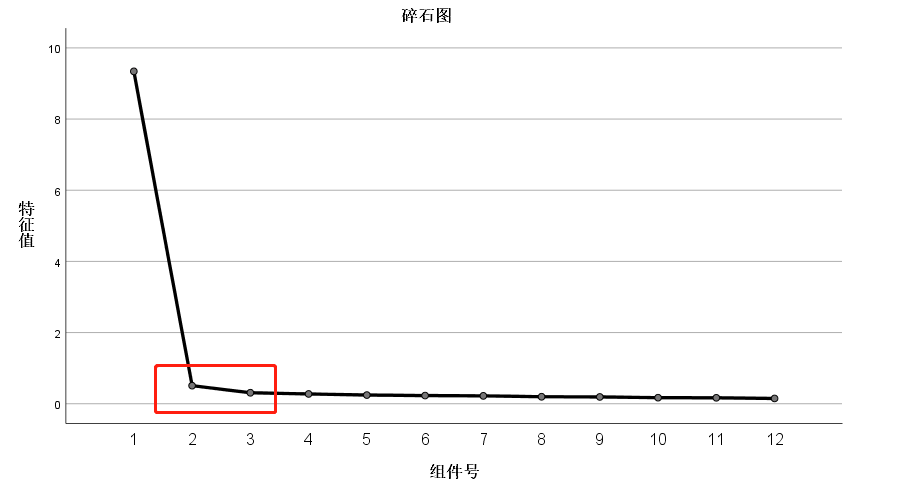
【碎石图】:各公因子与其对应特征值的折线图。
碎石图可以辅助判断因子提取个数。当折线由陡峭突然变得平稳时,陡峭到平稳对应的因子个数即为参考提取因子个数。如图所示,2个因子和3个因子之间的坡度变缓,说明第3个因子可解释信息较少,前2个因子已经可以涵盖大部分的信息,因此可选用因子个数为2;
提取:根据自身的需求进行选择
【基于特征值大于1】如果没有特征值大于1的成分,SPSS将不会为我们进行提取
比较适合探索分析。
特征值:是某公共因子对所有原变量载荷的平方和,它反映该公共因子对所有原始总变异的解释能力,等于因子载荷矩阵中某一列载荷的平方和。一个因子的方差贡献越大,说明该因子就越重要。
特征值小于1的因子通常被认为是不具有解释力的因子,因为它们对原始变量的方差贡献不如单个原始变量,甚至可能具有负面解释力。因此,通常建议将特征值小于1的因子剔除,以改善因子结构的解释力和稳定性。
但是,在实际应用中,是否可以直接剔除特征值小于1的因子还需要根据具体情况来决定。有时,特征值小于1的因子可能仍然具有一定的解释力,或者可以与其他因子组合成更有意义的复合因子。在这种情况下,可以考虑保留这些因子,并进行进一步的分析和解释。
【因子的固定数目】选择固定数目提取因子,那么无论因子特征值多少,SPSS都会为我们提取前几个固定的因子
比较适合已有一定的业务假设,对假设进行验证
【最大收敛迭代次数】:默认25不用修改
如果变量数众多,样本量巨大,建议将此数值改为999,以防出现迭代后未达到收敛标准的情况。
尽量使一个变量在较少的几个因子上有比较高的载荷,利用旋转使得因子变量更具有可解释性。
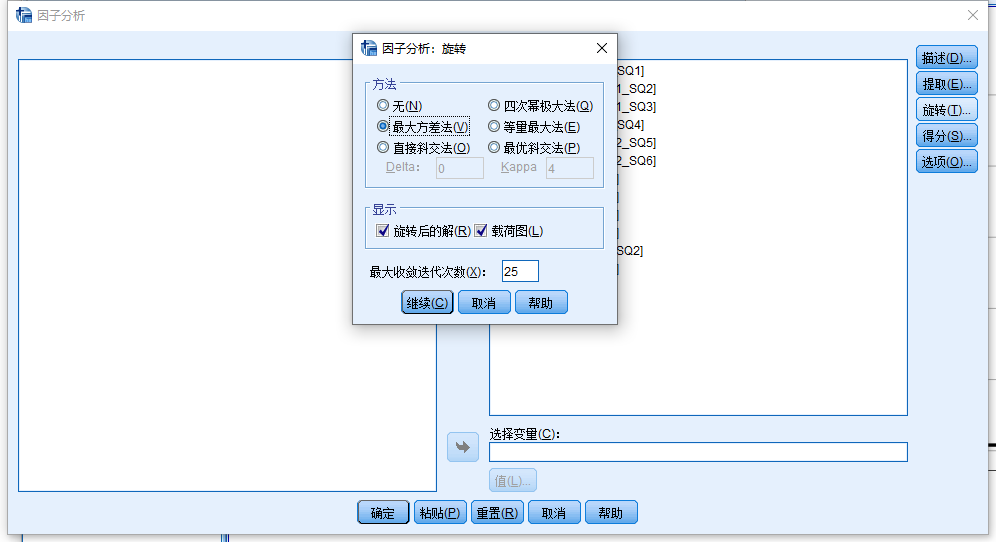
方法:
【最大方差法】:这是最常用的因子旋转的方法,该方法可以使每个变量尽可能在一个因子上有较高的载荷,而在其他的因子上载荷较小,从而因子更好地解释因子所包含的意义;
显示:
(1)【旋转解】:输出旋转之后的因子载荷矩阵。
(2)【载荷图】:将旋转之后的因子载荷矩阵以散点图形式在3维空间中表示出来。
局限性:最多图示旋转因子载荷矩阵的前3列,第4个因子及之后的载荷无法展示。
什么是载荷?
因子载荷:某个因子与某个原变量的相关系数,主要反映该公共因子对相应原变量的贡献力大小。
(以下内容选读)
统计意义来看,假如从p个变量的数据文件进行因子分析得到m个共同因子,那么m个共同因子的变化可以解释各个变量的大部分变异,换句话说,用这m个因子可以在相当程度上预测每一个变量的变化。于是得到下列回归方程组:
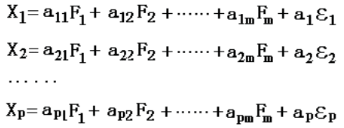
该方程组表示了得到m 个公共因子后,就可以使用这些公共因子在一定程度上预测每一个观测变量。方程中的系数正好是相对应的观测变量与公共因子的相关系数,也叫做该观测变量在对应因子上的载荷,即因子载荷,它反映了二者的关系强度。
aij 的统计意义就是第i个变量与第 j 个公共因子的相关系数即表示 Xi 依赖 Fj 的份量(比重)。统计学术语称作权,心理学家将它叫做载荷,即表示第 i 个变量在第 j 个公共因子上的负荷,它反映了第 i 个变量在第 j 个公共因子上的相对重要性。
如果只是为了达到变量的降维处理目的,此步骤可不需要。
因子得分可以用来评价每个个案在每个公共因子上的分值,该分值包含了原始变量的信息。
因子得分怎么计算?
计算因子得分首先将因子变量表示为原有变量的线性组合,即:
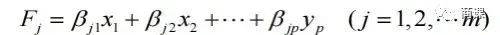
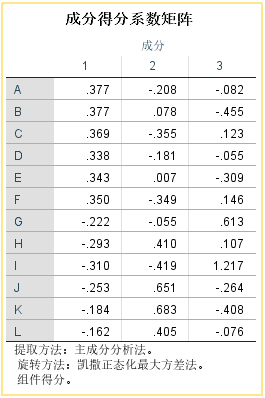
【成分得分系数矩阵】 :显示了每个变量在旋转后的成分中的得分权重。
该矩阵给出因子得分的计算公式,在表达式中各个变量已经不是原始变量而是标准化变量。旋转成分矩阵中,因子结构表达式可以将各变量表示为公因子的线性形式,也称为得分因子函数。最常用的估计法为“回归法”。
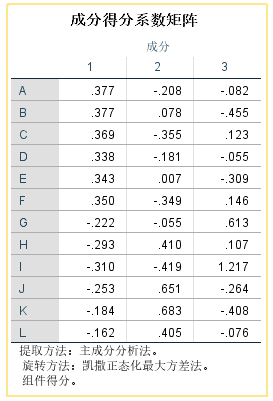
F1=0.377*A+0.377*B+0.369*C+0.338*D+0.343*E+0.350*F+......
前面已经按了保存为变量就无需手动计算了
基于因子得分的综合分析
最后一步,如有需要:保存公因子得分进行综合评价。
什么情况下会用到:在市场研究中,在横向比对不同产品的表现时,如果需要一个综合得分;其他如城市经济学研究中,涉及到各个地区的综合得分情况时,也会用到,适用范围很广泛。
怎么计算呢?
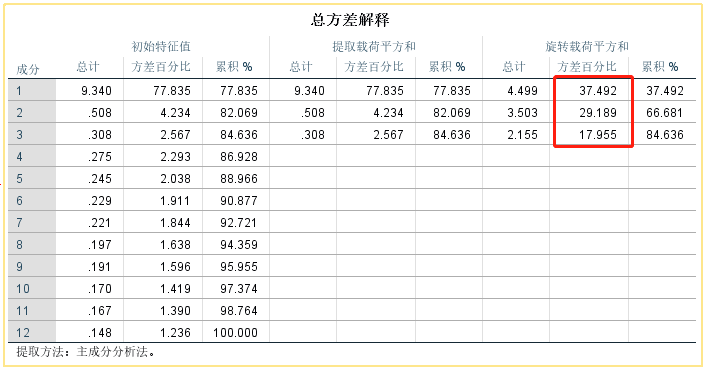
综合评分主要基于各公因子所对应的方差贡献率比例为权重来计算,公式为:综合得分=各因子方差百分比/总方差百分比*因子得分
Score=37.492/84.636*FAC1_1+29.189/84.636*FAC2_1+17.955/84.636*FAC3_1
FAC X_1即为前叙的因子得分
至此,基本上已完成因子分析的全流程梳理,以上截图表格按照操作步骤均会自动产出。
描述统计:基础内容,不做解读。
相关性矩阵:初步了解各变量之间的相关性。
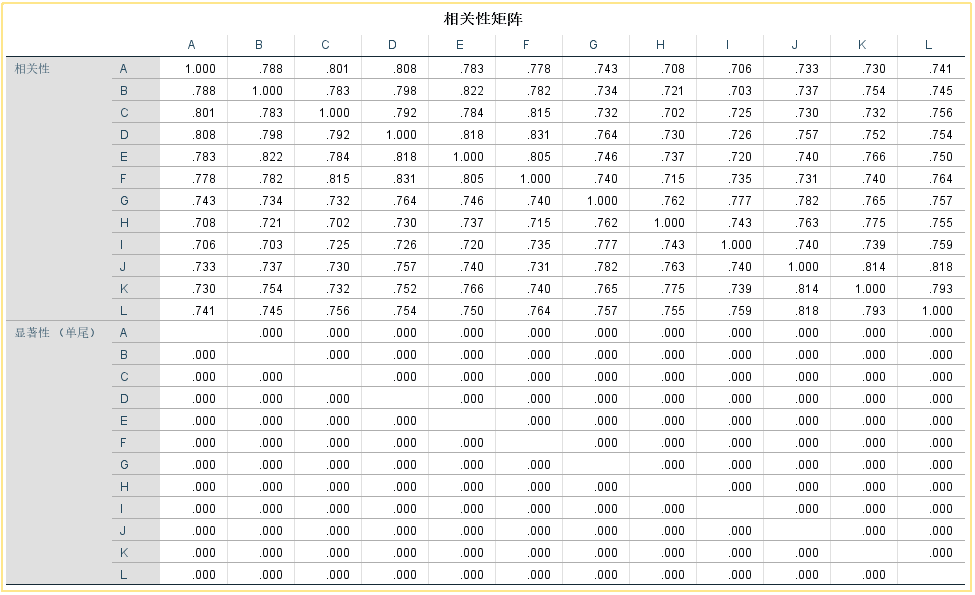
相关性矩阵:KMO值>0.8,,巴特利特球形检验Sig.<0.05,表明适合做因子分析。

公因子方差:提取的3个公因子能够解释A信息的82.3%,其他变量同理。该列的值越接近1表明公因子提取的效果越好。
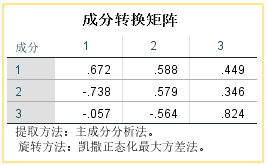
总方差解释:
【总计】:各公因子的特征值;
【方差百分比】:表示各公因子的相对重要性;
【累积%】:对应位置及该位置以上的所有公因子对原始变量的解释程度;
【初始特征值】:显示提取等于原始变量个数公因子的特征值、方差与累计方差贡献率。本例中有12个变量,则显示提取12个公因子的特征值、方差与累计方差贡献率(该列系统默认显示)。
【提取载荷平方和】:表示提取设定个数下未旋转公因子的特征值、方差与累计方差贡献率。本例提取了3个公因子。
【旋转载荷平方和】:表示提取设定个数下旋转公因子的特征值、方差与累计方差贡献率。
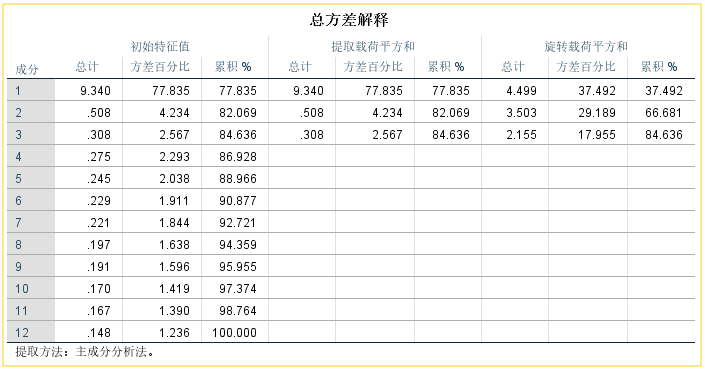
成分矩阵:显示未旋转的成分载荷矩阵。每一个元素都代表相关系数,例如0.881是A与公因子F1的相关系数。
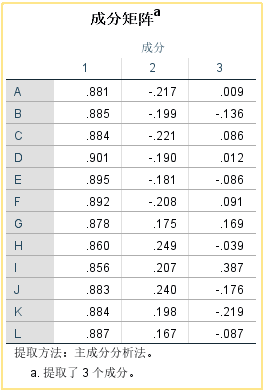
旋转后的成分矩阵:显示旋转的成分载荷矩阵。每一个元素都代表相关系数,例如0.752是A与公因子F1的相关系数。
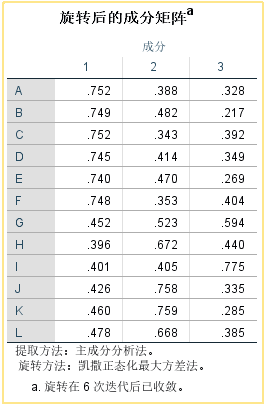
成分转换矩阵:利用成分转换矩阵,可以实现旋转载荷阵与未旋转载荷阵之间的相互转换。如若无特殊需要,并无实际分析价值。
成分得分系数矩阵:显示计算因子得分的系数。
成分得分协方差矩阵:显示了旋转后的成分得分之间的协方差。在表格中,每个单元格的值表示对应成分之间的协方差。
可以观察到成分1和成分2之间的协方差为0,即它们是无关的或不相关的。这表示旋转后的成分是相互独立的,可以单独进行分析和解释。
抽象理解:
因子分析方法主要用于三种场景,分别是:
信息浓缩:将多个分析项浓缩成几个关键概括性指标。
权重计算:利用方差解释率值计算各概括性指标的权重。
综合竞争力:利用成分得分和方差解释率这两项指标,计算综合得分。
具体实践:
因子分析+聚类分析:市场细分
通过对提取的因子做聚类分析将受访者分成不同的人群,考察不同人群在人口、社会、经济学等方面的特征,寻找并描述自己的目标市场。
因子分析+回归分析:满意度研究
满意度研究需要设计变量众多、层次分明的满意度指标体系,为了使问卷设计得合理科学,必须在满意度研究的预调查阶段对指标设置的合理性进行检验:
因子分析+知觉图:品牌研究
因子分析可以从研究品牌形象的诸多软性和硬性的特性中浓缩和提炼的出少数几个综合因素,用较低的维度直观展示属性之间、对象之间及对象与属性之间的关系,使得品牌形象更加鲜明,而因子分析的结果可以用定位图的方式呈现。
举例:如品牌与属性之间的关系,对某一受访者对某一品牌在每一属性上的评分(是&否)看成是因子分析的一个样本,在进行因子分析后(base为总人次),每一个品牌在每一个因子上的得分高低,即所有评价该品牌的被访者的因子得分之均值,称为该品牌的平均因子得分。
因子分析+相关性:忠诚度研究
因子分析可以从满意度研究的诸多因素中浓缩和提炼出几个互不相关的综合指标,它们反映了满意度研究不同侧面的内容,同时也涵盖了原有指标的大部分信息。
把提取的因子和忠诚度的有关指标进行相关性的研究,我们可以发现那些有助于提高用户忠诚度的关键所在,从而使工作更具有目标性。
“继续使用、增加使用、推荐使用”是体现用户忠诚度的三个由低到高的层次,不同层次的忠诚表现会给企业增加不同程度的收益。
参考文献:
①《市场研究中的统计分析方法》.郑宗成/张文双/黄龙/张章新
②《多元统计分析》.刘婧媛
③《探索性因子分析》.安洁勇/西恩·比尔斯