前述的所有聚类方法中，变量的类型均为数值变量，如何对同时存在分类变量和数值变量进行聚类分析？

对同时存在分类变量和数值变量的数据进行聚类分析可以通过以下两个主要思路来实现：

Method 1：将分类变量转换为数值变量，采用适合数值变量的聚类方法。

Method 2：采用适合混合变量的聚类方法。

分类变量转数值，用数值变量的聚类方法

这种方法的关键在于如何将分类变量合理地转换为数值形式，以便可以使用诸如K-means、DBSCAN等适合数值变量的聚类算法。以下是常见的编码技术：

1. 独热编码（One-Hot Encoding）

将每个分类变量转换为多个二进制变量，每个变量对应一个可能的取值。尤其适合类别之间没有固有顺序或大小关系的名义变量。

具体到“红”、“绿”、“蓝”的例子，独热编码会这样表示：

• 红色：[1, 0, 0]
• 绿色：[0, 1, 0]
• 蓝色：[0, 0, 1]

每个颜色就转换成了一个唯一的向量，且向量之间的差异（如欧氏距离）能准确反映类别间的不相交特性，有助于算法理解和处理这些类别特征。

优点：保留了分类变量的所有信息，且不会引入虚假顺序关系。

缺点：当分类变量的取值较多时，会导致维度爆炸。

2. 标签编码（Label Encoding）

标签编码将分类变量的每个取值映射到一个唯一的整数。这种方法适合有序分类变量（Ordinal Variables），但不适合无序分类变量，因为它会引入顺序关系。

这种方法适合于那些类别之间存在自然排序或者有意义的顺序关系的情况。

比如教育程度（高中、大学、研究生）可以被编码为0、1、2，因为这里存在一个明确的顺序。

优点：简单直接，适合有序分类变量。

缺点：对于无序分类变量，可能会引入虚假的顺序关系。

3. 频率编码（Frequency Encoding）

频率编码将每个分类变量的取值替换为其在数据集中出现的频率。这种方法可以在一定程度上反映类别的重要性。

本身是一种灵活的处理分类特征的方法，适用于那些类别频率本身含有重要信息的场景。

假设有一个分类变量“产品类型”，取值为“电子”、“家具”和“服装”，出现频率分别为0.4、0.3和0.3。频率编码后为：

• 电子：0.4
• 家具：0.3
• 服装：0.3

优点：

减少维度：与独热编码相比，频率编码不会增加特征空间的维度，这对于维度已经很高的数据集特别有用。

捕获频率信息：编码后的特征直接携带了类别出现的频率信息，这在某些情况下对模型是有益的。

缺点：

丢失类别间的独立性：如果类别间的频率接近，编码后的数值可能无法很好地区分它们，可能导致模型学习的类别关系与实际情况有偏差。

对极端值敏感：如果某个类别出现得非常频繁或非常稀少，其频率编码的值可能会过度影响模型。

4. 二元编码（Binary Encoding）

先将分类变量进行标签编码，再将标签编码转换为二进制表示，每个位作为一个新的特征。

适用于分类变量取值较多且需要控制特征数的场景，避免维度爆炸。

假设我们有一个分类变量“城市”，取值为“A”、“B”、“C”、“D”。

步骤1：标签编码

首先，将每个城市的取值映射为一个整数标签：

• A -> 1
• B -> 2
• C -> 3
• D -> 4

步骤2：二进制转换

接着，将这些整数标签转换为二进制表示：

• 1 -> 01
• 2 -> 10
• 3 -> 11
• 4 -> 100

实际情况下，我们通常需要所有二进制表示的位数相同（补零），例如，前面补零成3位表示：

• 1 -> 001
• 2 -> 010
• 3 -> 011
• 4 -> 100

步骤3：生成二进制特征

最后，将每个位作为一个新的特征列：

• 城市_A：1 -> 001
• 城市_B：2 -> 010
• 城市_C：3 -> 011
• 城市_D：4 -> 100

生成的特征表如下：

优点：

减少维度：相比独热编码，二元编码大大减少了编码后的特征数，减少维度爆炸

例如，对于8个不同类别，独热编码需要8个二进制特征，而二元编码仅需3个二进制特征（因为3位二进制数可以表示8个不同的值）。

避免多重共线性：二元编码不会像独热编码那样引入多重共线性问题，因为二元编码生成的特征是相对独立的。

缺点：

解释性较弱：二元编码生成的特征不如独热编码直观，难以解释。

实现复杂：需要进行标签编码和二进制转换，步骤稍显复杂。

采用适合混合变量的聚类方法

直接使用适合处理混合变量的聚类方法是另一种解决方案。这些方法能够处理数值变量和分类变量，避免了对分类变量进行编码转换的复杂性。

1. K-prototypes聚类

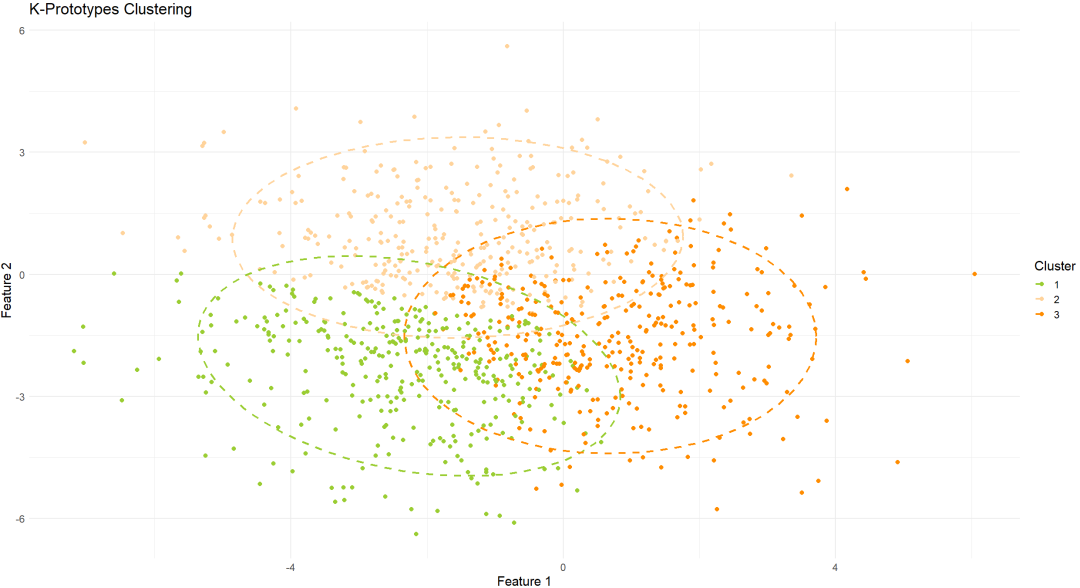
K-prototypes聚类是K-means和K-modes的结合，专门设计用于混合数据。它通过结合欧氏距离（用于数值变量）和汉明距离（用于分类变量）来计算聚类中心。

步骤：

1. 初始化K个聚类中心，包含数值变量的均值和分类变量的众数。
2. 根据综合距离（数值变量用欧氏距离，分类变量用汉明距离）将数据点分配到最近的聚类中心。
3. 更新聚类中心，重新计算数值变量的均值和分类变量的众数。
4. 迭代步骤2和3，直到聚类中心稳定。

实现工具

Python：kmodes库实现K-Prototypes聚类。

R：clustMixType包来实现K-Prototypes聚类。

SPSS：使用 SPSS Modeler，通过 Python 或 R 脚本节点来实现 K-Prototypes 聚类。

注意事项

需要合理选择 k 值和 γ 参数。

k 值负责聚类数量。

γ 参数负责平衡数值变量和类别变量的重要性。

拓展：γ参数

用于平衡数值属性和类别属性在距离度量中的重要性。由于数值属性和类别属性的度量单位和范围不同，它们对距离计算的影响也不同。通过调整 γ 参数，可以控制类别属性在总体距离中的权重，使得算法能够更加合理地处理混合类型的数据。

具体来说，K-Prototypes 聚类的综合距离公式为：

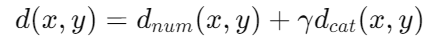
γ 参数在这里起到一个权重平衡的作用，决定了类别属性对距离计算的贡献程度。γ 值较大，类别属性在距离度量中的影响就较大，反之亦然。

调整 γ 参数的原则

1. 数据特征：如果数据集中数值属性较多，且在聚类过程中更重要，可以选择较小的 γ 值，反之亦然。
2. 聚类结果评估：通过实验评估不同 γ 值对聚类结果的影响。
3. 领域知识：根据领域知识和实际应用需求，确定数值属性和类别属性的重要性。

特别说明：γ 参数并不是用于调整单独变量的权重，而是用于调整数值变量整体与类别变量整体的权重。

在R可以通过调整不同的 γ 参数来查阅最终聚类效果

# 示例数据集data <- data.frame(  年龄 = c(23, 45, 25, 30, 35, 50),  性别 = c('男', '女', '男', '女', '男', '女'),  收入 = c(40000, 50000, 42000, 48000, 45000, 52000),  购买偏好 = c('电子产品', '化妆品', '电子产品', '服装', '服装', '化妆品'))# 将性别和购买偏好转换为因子类型data$性别 <- as.factor(data$性别)data$购买偏好 <- as.factor(data$购买偏好)# 定义不同的 gamma 值gamma_values <- c(0.5, 1, 2, 5)

因子类型是什么？

因子（Factor）类型是 R 语言中专门用于处理类别数据（Categorical Data）的一种数据类型。

因子类型在内存中会使用整数来存储每个类别的水平，这种方式在数据量大时更加节省内存，提高计算效率。

同时有助于算法正确处理这些变量，避免将其视为连续数值。

2. Gower距离结合层次聚类

Gower距离是一种适用于混合数据的距离度量，可以处理数值、分类和二元变量。使用Gower距离计算距离矩阵，然后应用层次聚类方法（如凝聚层次聚类）进行聚类。

步骤：

1. 计算Gower距离矩阵，综合考虑数值变量的归一化欧氏距离和分类变量的简单匹配系数。
2. 使用凝聚层次聚类方法构建聚类树。
3. 根据预定的聚类数目或距离阈值截取聚类树，得到最终的聚类结果。

3. Self-Organizing Maps (SOM)

Self-Organizing Maps是一种基于神经网络的无监督学习方法，可以将高维数据映射到低维空间。SOM可以处理混合变量，但需要对数据进行适当的标准化。

步骤：

1. 数据预处理：将数值变量标准化，分类变量进行独热编码或其他适当的编码。
2. 初始化SOM网络的权重。
3. 训练网络：逐步调整网络权重，使其匹配输入数据的拓扑结构。
4. 根据SOM的输出，将数据点分配到相应的聚类。

4. 混合高斯模型(GMM)

混合高斯模型假设数据点由多个高斯分布组成，主要用于数值变量，但可以通过扩展处理混合变量。

步骤：

1. 初始化每个高斯分布的参数（均值、协方差和混合系数）。
2. 期望步骤（E-step）：计算每个数据点属于每个高斯分布的概率。
3. 最大化步骤（M-step）：根据E-step的结果，更新高斯分布的参数。
4. 迭代E-step和M-step，直到收敛。

其他拓展方法

使用混合模型或集成方法

混合模型和集成方法可以结合多种聚类算法的优点，提供更稳健和灵活的聚类结果。

① Ensemble Clustering

集成聚类方法通过结合多个不同聚类算法的结果，生成更稳健聚类结果。常见集成方法包括共识聚类和聚类集成。

② 贝叶斯混合模型

贝叶斯混合模型使用贝叶斯方法结合多种高斯分布，适用于处理复杂分布和混合变量。

使用深度学习技术

近年来，深度学习在处理复杂和高维数据方面展现了强大的能力。使用深度学习技术进行聚类是一种新兴的方法，适用于大规模和复杂数据集。

① 自编码器

自编码器是一种无监督的神经网络，可以将高维数据压缩到低维表示，同时保留重要的结构特征。通过自编码器进行降维后，可以应用传统的聚类算法。

② 深度嵌入聚类(DEC)

DEC结合自编码器和聚类算法，通过联合优化降维和聚类目标函数，直接在低维空间中进行聚类。