基础认识

谱聚类算法是一个使用起来简单，但是讲清楚却不是那么容易的算法。

谱聚类（Spectral Clustering）是一种基于图论的聚类算法。

图论是数学的一个分支，专注于研究图（Graphs）这种抽象数据结构。

谱聚类算法是利用矩阵的特征向量进行聚点的聚类算法。

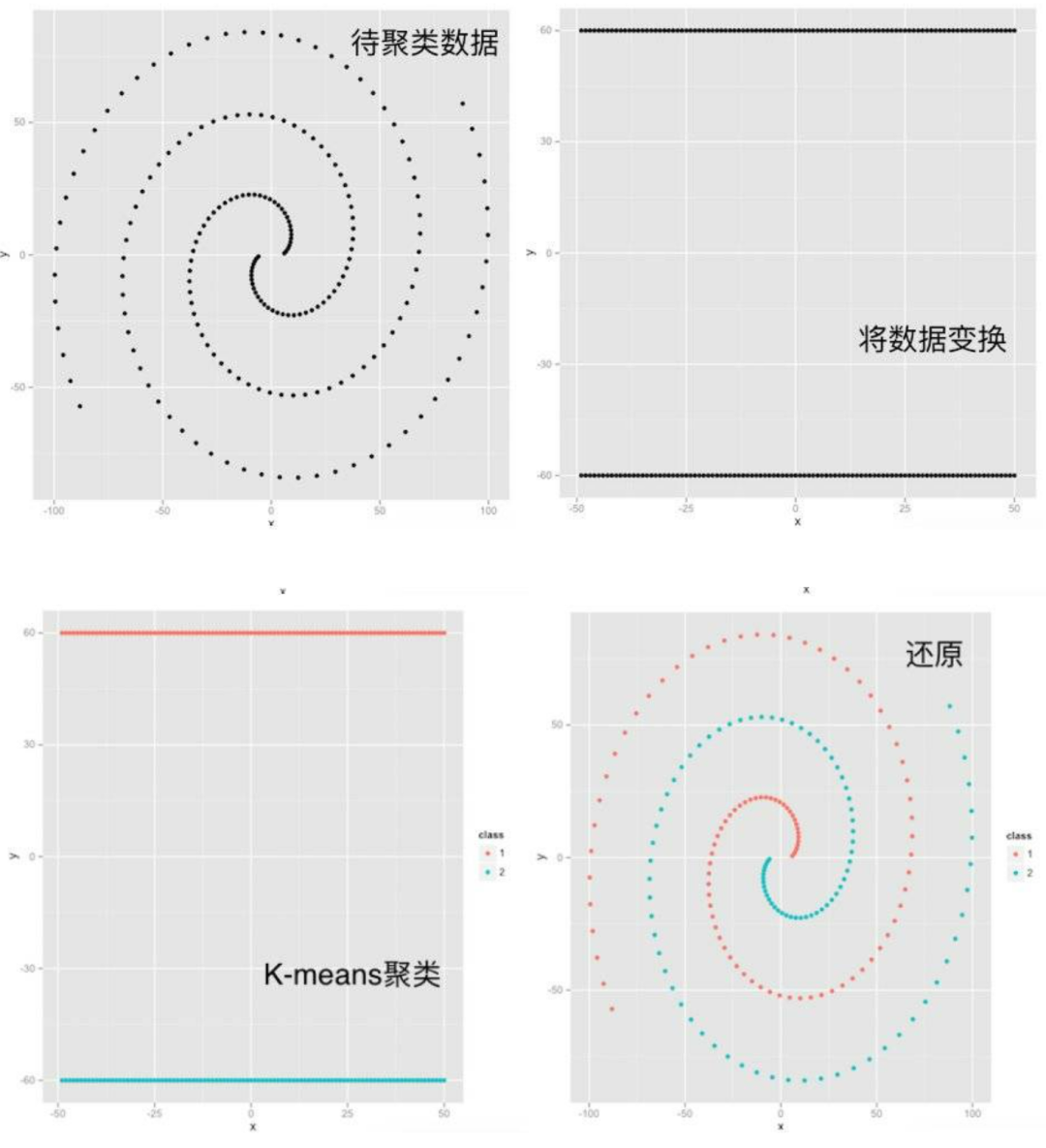
谱聚类是一种基于降维的聚类算法，它由两部分组成：

第1部分是对数据进行一定的变换，使得交织在一起的数据分开。

第2部分是使用传统的K-means等算法对变换后的数据聚类。

以比喻的方式理解一下：谱聚类就像是在一张错综复杂的社交网络图上寻找紧密相连的小团体。通过分析每个人与其他人的互动频率（边的权重），构建出一张反映关系强度的图，然后通过数学手段找出那些自然形成的圈子，即聚类。

在市场细分中，我们可以将每个用户视为一个节点，用户之间的购买行为或偏好相似度作为边权重，通过谱聚类算法将用户划分为不同的群体。

原理

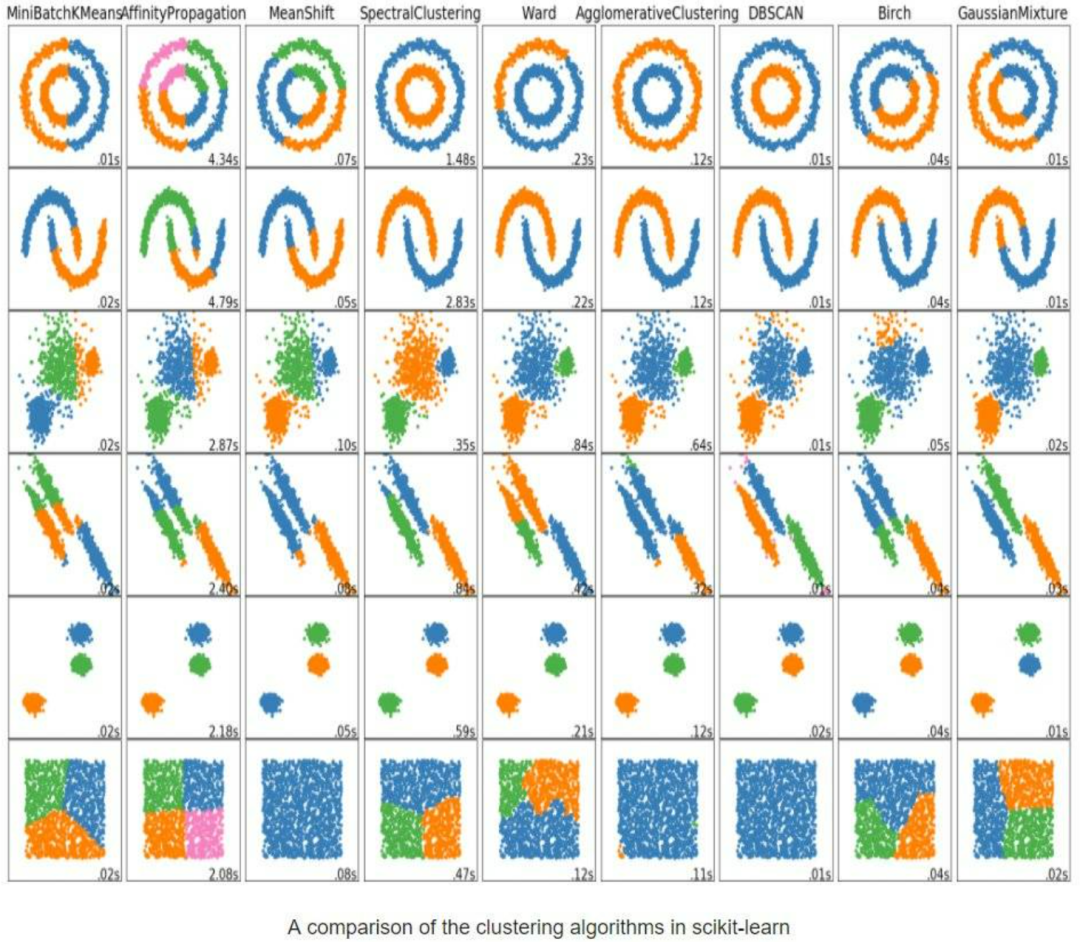
从数学角度来看，谱聚类算法可以看作是对数据点之间相似性的一种度量。

谱聚类的核心思想是将数据集视为一个图，其中每个数据点是一个节点，节点之间的连接强度（边的权重）表示它们之间的相似度或距离（距离越远，边权重越低，反之亦然）。将数据点之间的相似性转化为图的邻接矩阵的特征值和特征向量，然后对特征向量划分（让切图后不同的子图间边权重和尽可能的低，而子图内的边权重和尽可能的高）来实现聚类。

数学上，谱聚类涉及以下几个关键概念：

①相似性矩阵（相似矩阵）：表示数据点之间的相似度。

②度矩阵（D）：对角矩阵，对角线上的元素是相似性矩阵每一行（或列）的和。

③拉普拉斯矩阵（L）：定义为 L = D - WL=D−W，其中 WW 是相似性矩阵。

④特征分解：对拉普拉斯矩阵进行特征分解，得到最小的几个特征值和对应的特征向量。

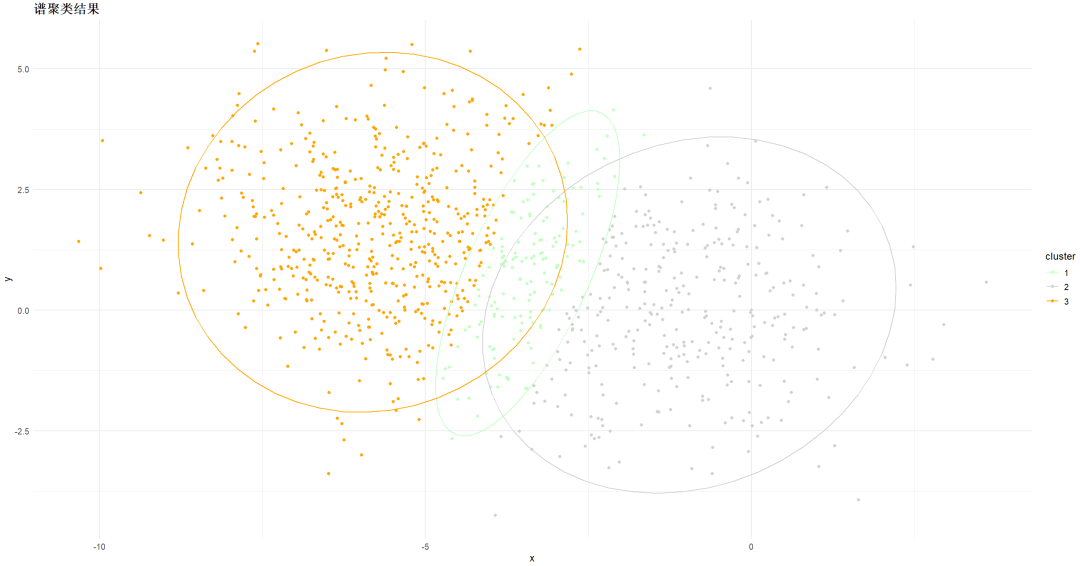
详细步骤如下：

① 数据预处理：如数据标准化处理，使其具有零均值和单位方差。

② 构建相似度图：根据数据点之间的相似度构建一个权重矩阵。

③ 计算拉普拉斯矩阵：基于相似度矩阵构建拉普拉斯矩阵，它描述了图中顶点的连接关系和顶点的度数。

④ 特征值分解：求解拉普拉斯矩阵的前k个最小非零特征值对应的特征向量，提取主要特征向量构成特征向量矩阵。

⑤ 映射：用这些特征向量将原始数据映射到低维空间。

⑥ 聚类：将特征向量矩阵的每一行看作是高维空间中的一个点，在低维空间中使用传统的聚类算法（如K-means）进行聚类。

前提条件

① 数据具备相似性：数据集需要有足够的相似性信息，以构建相似性矩阵，如果数据点之间没有相似性，那么谱聚类算法将无法进行有效的聚类。

② 相似度度量方式：需要合适的相似度度量方式来构建相似度矩阵，度量方式不同得到的图拉普拉斯矩阵不同，可能会导致不对称。

③ 预设聚类个数：谱聚类算法需要预先设定聚类的个数。

④适用于数值型变量：其他变量类型需要进行适当转换。

优势

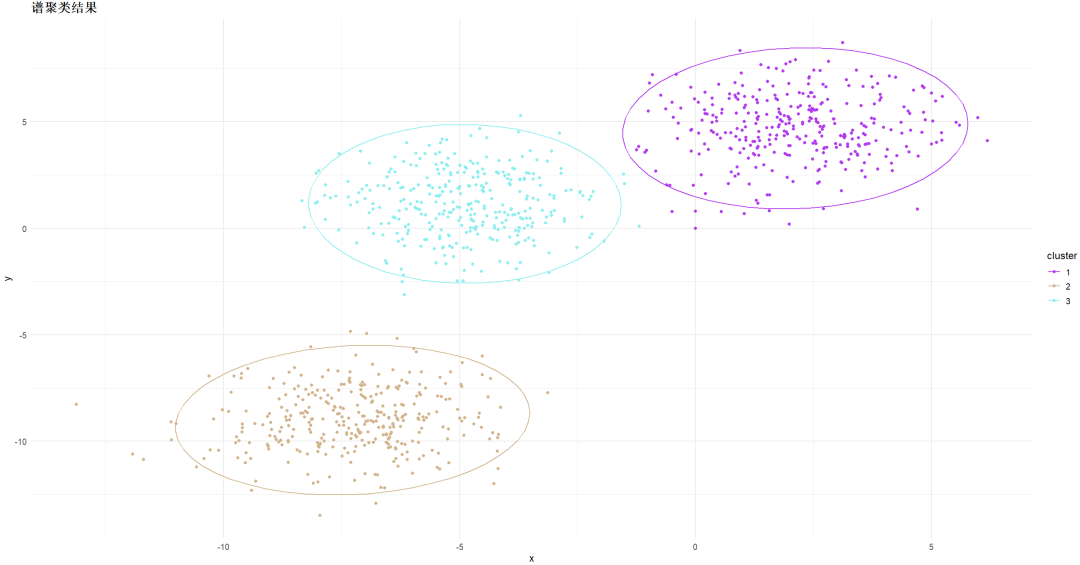
① 能够处理任意形状的聚类，并且不需要预先指定聚类的形状。

② 能处理高维复杂数据，可以自然地将高维数据映射到低维空间，实现降维。

③ 对噪声和异常值具有较强的鲁棒性，对于处理稀疏数据更有效（谱聚类只需要数据之间的相似度矩阵）。

劣势

① 对参数敏感，特别是相似度度量和聚类数目的选择。

聚类效果依赖于相似矩阵，不同的相似矩阵得到的最终聚类效果可能很不同。

实现工具

Python中的scikit-learn、networkx、numpy和scipy等库。

R中如cluster, igraph, 或专门的谱聚类包如spectralClustering（但还没找到对应的加载包）。

以R的kernlab包执行。

在kernlab包中，用于执行谱聚类的函数是specc。

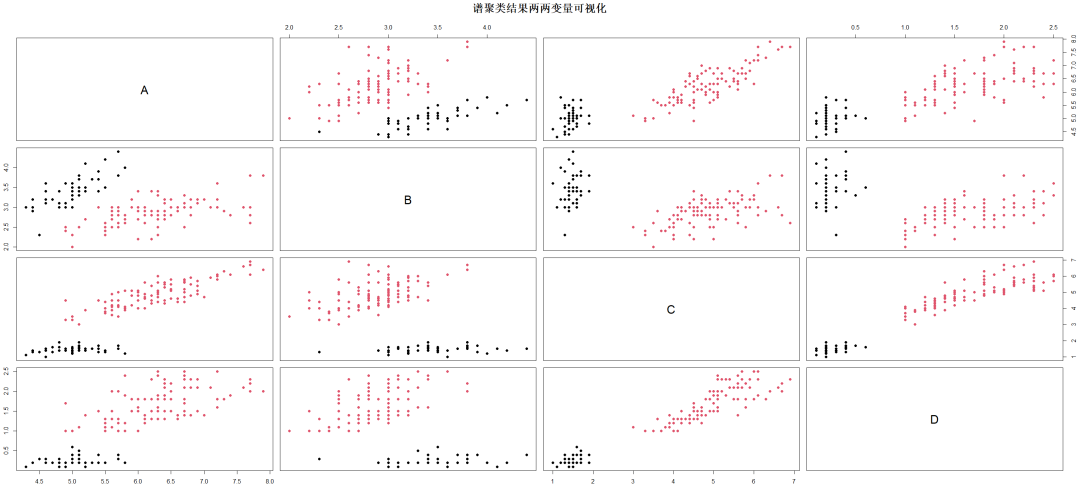
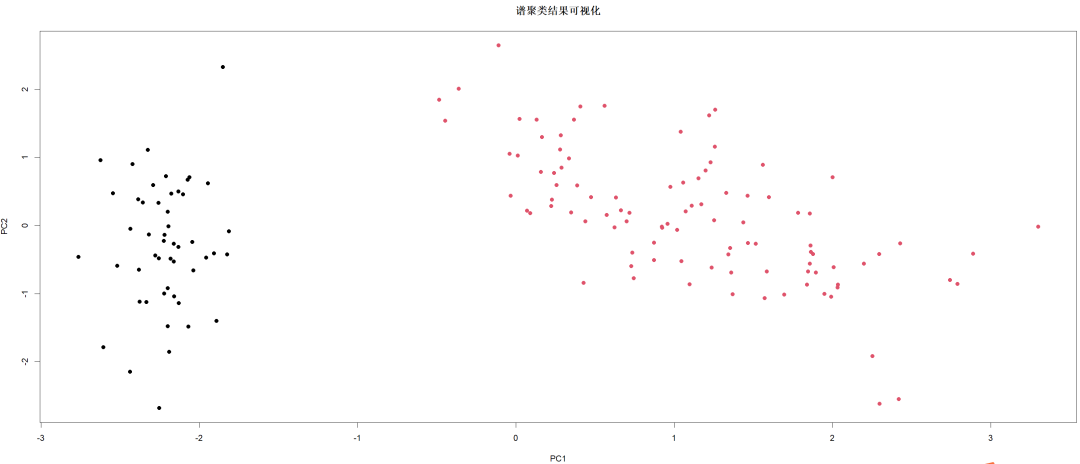
延伸拓展：

① 传统谱聚类（如基于图的拉普拉斯矩阵方法）

优势：对于处理具有明确定义的局部结构和易于用图表示的数据集非常有效。

局限性：在面对非线性可分数据时，标准的谱聚类可能无法有效捕获数据的内在结构，它主要基于线性变换。

② kernlab中的核化谱聚类

优势：通过引入核技巧，能够在高维甚至无限维特征空间中进行聚类，特别适合处理非线性数据分布。这种方法能够发现数据中的非线性结构，提供更为灵活的聚类边界。

局限性：计算复杂度相对较高，选择合适的核函数及其参数是挑战，错误的选择可能导致较差的聚类效果。

适用范围

①如果数据集主要表现出线性可分的结构，传统谱聚类可能就足够，并且计算效率更高。

②当数据集存在复杂的非线性结构时，kernlab中的核化谱聚类可能会提供更好的聚类性能。

结果如何评估

① 内部评价标准：如轮廓系数等其他聚类算法通用的评价指标。

② 外部评价标准：评估聚类结果是否与真实标签、过往数据一致。

应用场景

市场细分：将市场中的消费者分为不同的细分群体，以便更好地制定营销策略。

社交网络分析：可用于识别社交网络中的社区结构和群体特征，提供个性化推荐。

图像分割：可以根据像素之间的相似性构建图，使用谱聚类算法进行区分分割。

文本挖掘：可以根据文档之间的相似性构建图，使用谱聚类算法发现主题和分类。

其他说明

谱聚类是要求切图耗费的能量最少(对应前几个最小特征值)。

PCA的目的是用最少的特征尽可能地表示最多的信息(对应前几个最大的特征值)。