
两步聚类,又名二阶聚类,英文名称为TwoStep Cluster。
它结合两种不同的聚类技术,首先将数据进行预聚类,然后在此基础上进行最终的聚类分析。
可同时处理类别变量和连续变量,自动进行聚类类别数确定。
其设计初衷就是为了在面对复杂的数据类型时提供一种高效且准确的聚类方法。
Step1:初始时,所有数据点被认为是一个簇。算法会尝试将这个簇分成两个较为粗糙的子簇,通常是通过某种距离度量来完成。
Step2:在第一步得到的较粗的簇的基础上,进一步细化每个簇。这个过程可能会涉及合并一些相似子簇或者进一步分裂某些子簇,直到满足某种终止条件为止。
第一步的粗略聚类有助于减少数据的规模和复杂性,而第二步的细致聚类则确保了聚类结果的准确性和可靠性。
① 个案的排序必须完全随机,因为各案例在聚类特征数上的定位只有一次。
② 两步聚类算法设计用于处理大规模数据集,如果数据集规模较小,可能无需使用。
③适用于同时包含数值型和分类型变量的数据集。
④ 变量之间的相关性不应过高。
① 可同时基于类别变量和连续变量进行聚类。
② 可自动确定最终的分类个数。
③ 可处理大型数据集。
④ 结果稳定,不易受初始条件影响。
⑤ 两步聚类算法通过分阶段处理数据,有效降低了计算复杂度。
① 相比于单一的聚类算法,实现过程相对复杂。
② 初步聚类和最终聚类的簇数量选择对结果影响较大。
③对于高维度数据,聚类结果解释可能比较困难。
① 数据导入和预处理:加载数据,处理缺失值和异常值,进行标准化处理。
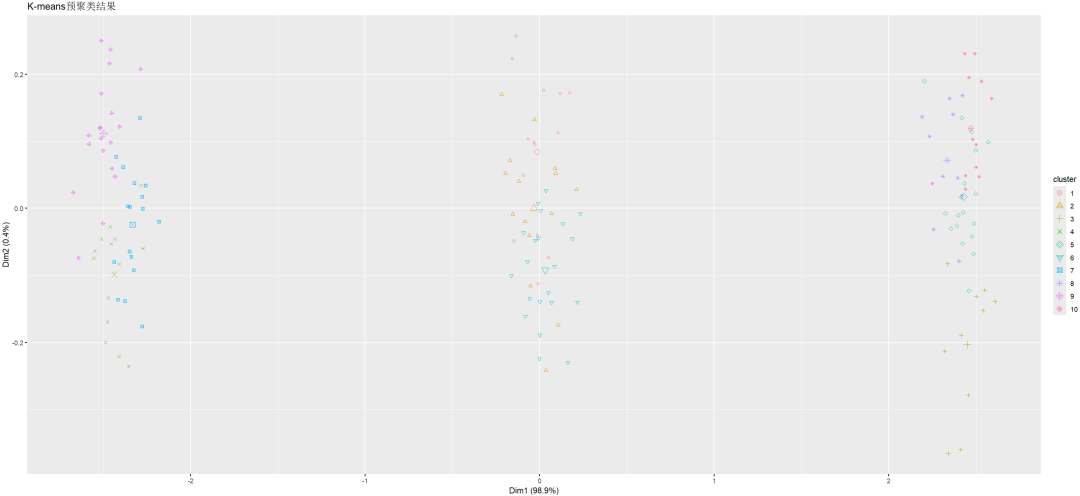
② 预聚类:使用快速聚类方法(如K-means)进行初步分组。
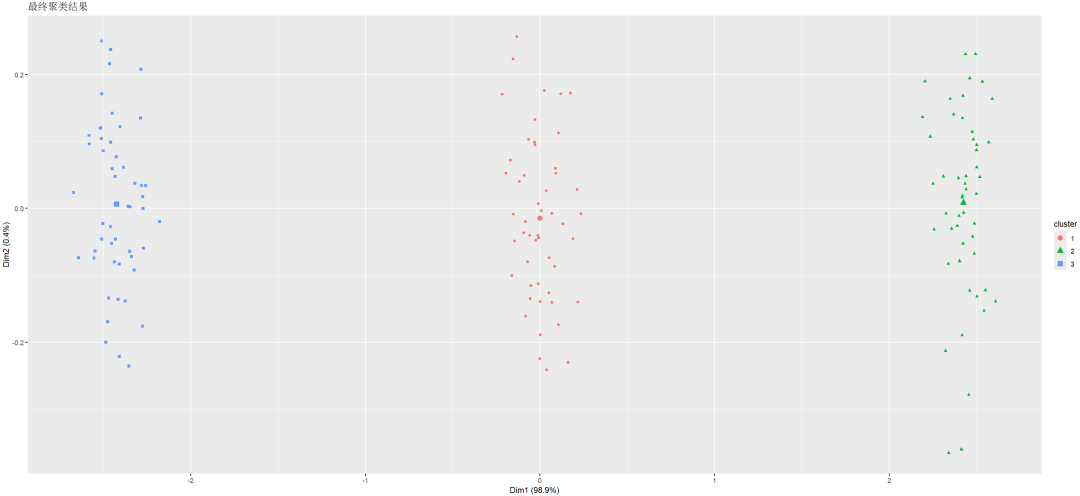
③ 二次聚类:选择适当的最终聚类算法,确定最终簇的数量并进行聚类。
④ 结果分析和可视化:对聚类结果进行分析和可视化,评估聚类效果。
两步聚类算法在SPSS中的实现是相对固定的,而在其他软件中则是相对灵活的。
SPSS
预聚类步骤:使用一种基于密度的自适应网格方法将数据划分为初始子簇。这一步骤使用了EM算法的思想,通过将数据分成多个子簇来减少数据量,并确定这些子簇的初始中心。
聚类步骤:使用改进的期望最大化(EM)算法对预聚类结果进行进一步的聚类分析。这种方法结合了K-Means和EM算法的优点,能够处理混合类型的变量,并提供更准确的聚类结果。
SAS
通常使用PROC FASTCLUS和PROC CLUSTER,但可以选择其他的聚类方法和步骤。
R
允许自由组合不同的聚类方法来实现两步聚类。
Python
可以自由选择和组合不同的聚类方法来实现两步聚类。
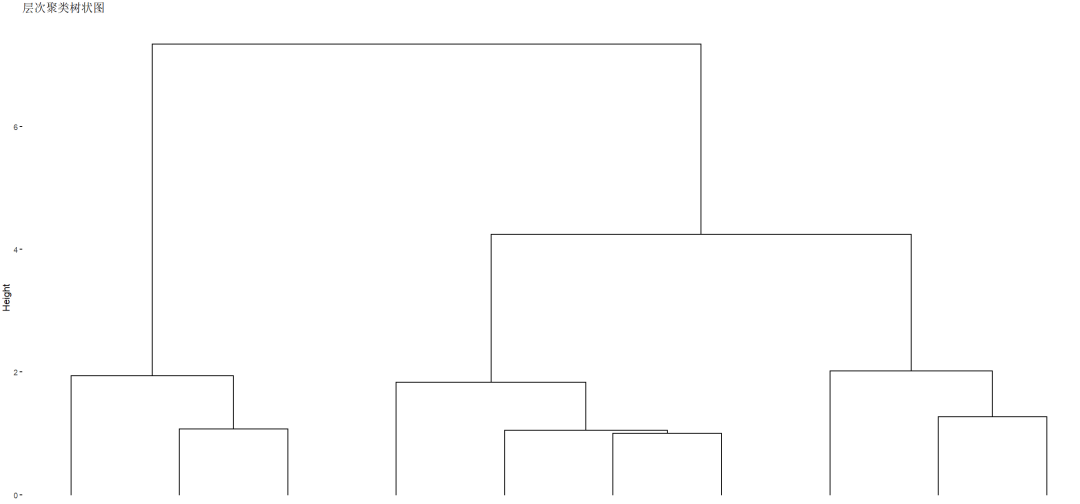
虽然均可灵活应用聚类算法,但很多情况下都会用快速聚类(如kmeans)做初步聚类,用层次聚类来进行二次聚类。
以K-means做了初步聚类。
以层次聚类做二次聚类(最终聚类)。
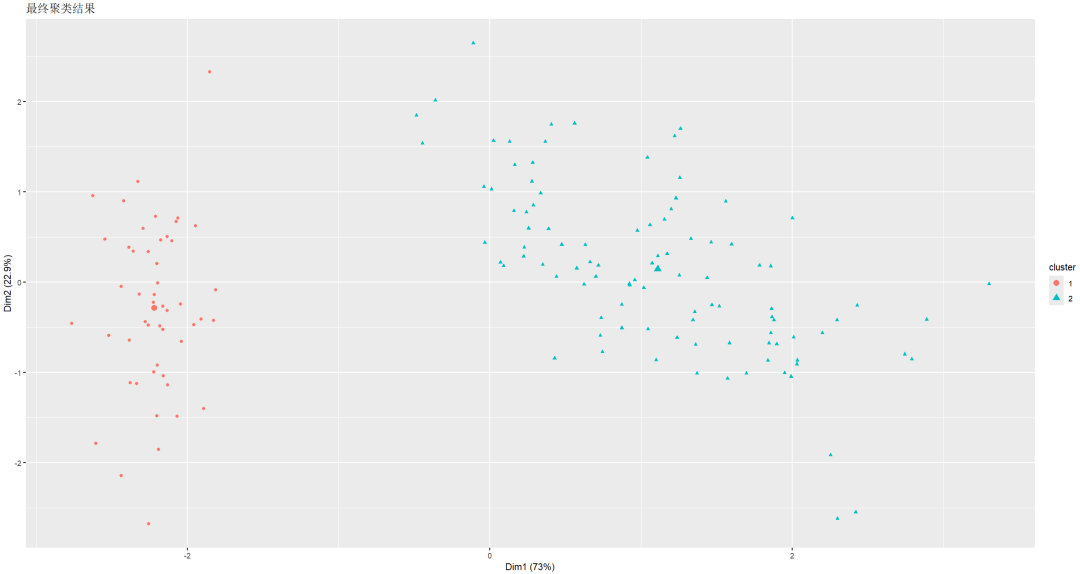
结果如何评估?
以下方法未穷尽,仅做举例。
① 轮廓系数:评估聚类结果的质量,范围为[-1, 1],越接近1表示聚类效果越好。
② 聚类误差(SSE):计算每个簇内数据点到簇中心的距离平方和,误差越小表示聚类效果越好。
③ 调整兰德指数(ARI):评估聚类结果与真实标签的匹配程度,范围为[-1, 1],越接近1表示匹配度越高。
应用数据集
SPSS默认自带数据集。
变量导入
把需要分析的变量导入到对应变量框中。
聚类数目
保持默认(无特殊诉求)。
距离测量
① 对数似然(Log-Likelihood):衡量统计模型拟合数据好坏的指标,评估和选择最佳的聚类方案。
对数似然是基于概率模型的,它计算了在给定聚类模型下,观测到当前数据的概率的对数。
在两步聚类分析中,通常使用对数似然比(Log-Likelihood Ratio)来比较不同的聚类方案,即比较两个或多个聚类方案的对数似然值的差异。 对数似然比越大,表示新的聚类方案相对于原来的方案提供了更好的数据拟合。
② 欧氏距离(Euclidean Distance):衡量个体之间的相似性或差异性。
在两步聚类分析中,欧氏距离作为个体之间相似性的度量,被用于第一步的聚类算法中,以确定哪些个体应该被分到同一个聚类中。在第二步中,每个大聚类内部的个体也会根据欧氏距离进行细分,形成更细致的聚类结构。
个体间的欧氏距离越小,表示它们越相似;距离越大,表示它们的差异性越大。
聚类准则
① 含义&作用
① 衡量模型拟合:它们提供了一种量化的方法来比较不同聚类模型的好坏。
② 复杂度惩罚:考虑了模型的复杂度,避免选择过于复杂的模型。
③ 指导模型选择:帮助确定最优的聚类数。
② AIC(赤池信息准则)
模型的复杂度(参数的数量)和模型的拟合优度(最大对数似然值)之间应该有一个平衡。AIC倾向于选择那些在拟合数据和模型复杂度之间取得最佳平衡的模型。 较小的 AIC 值表示较好的模型拟合。
③ BIC(贝叶斯信息准则)
BIC对模型复杂度的惩罚更加严厉,因为它与样本大小成正比。这意味着在样本量较大时,BIC倾向于选择更简洁的模型,更强调避免过拟合。
BIC 值越小表示模型的拟合效果越好。
它们都试图在模型的拟合优度和复杂度之间寻找一个平衡点。AIC更注重模型的拟合优度,而BIC则更倾向于选择简单的模型。
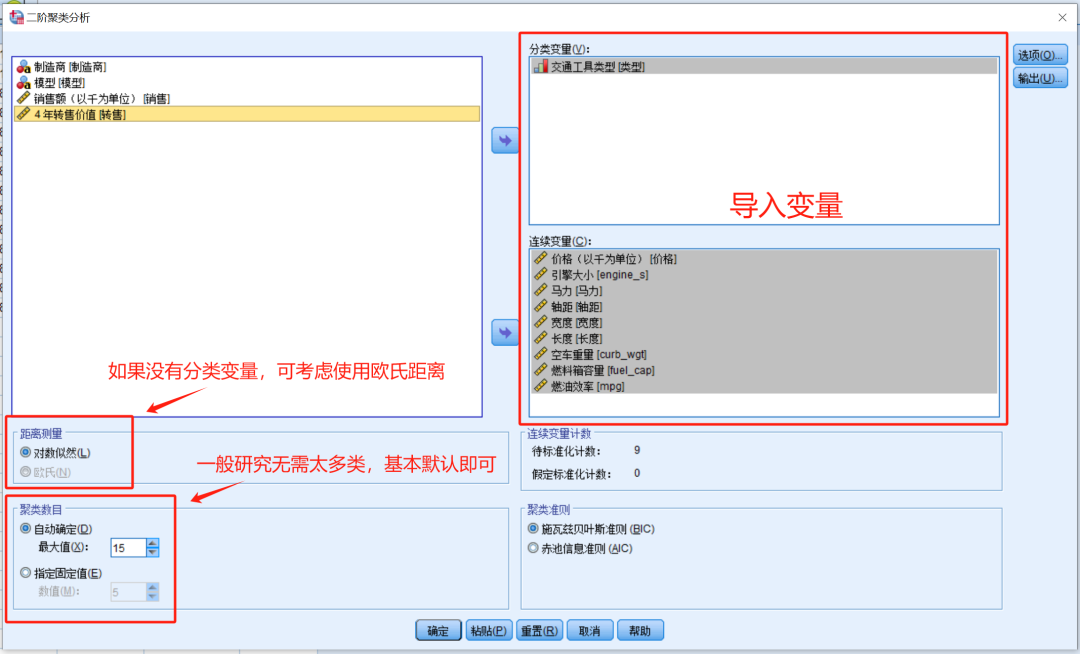
离群值处理
离群值是指那些与数据集中其他观测点显著不同的数据点。
若已进行相应的数据清洗,则无需勾选噪声处理。
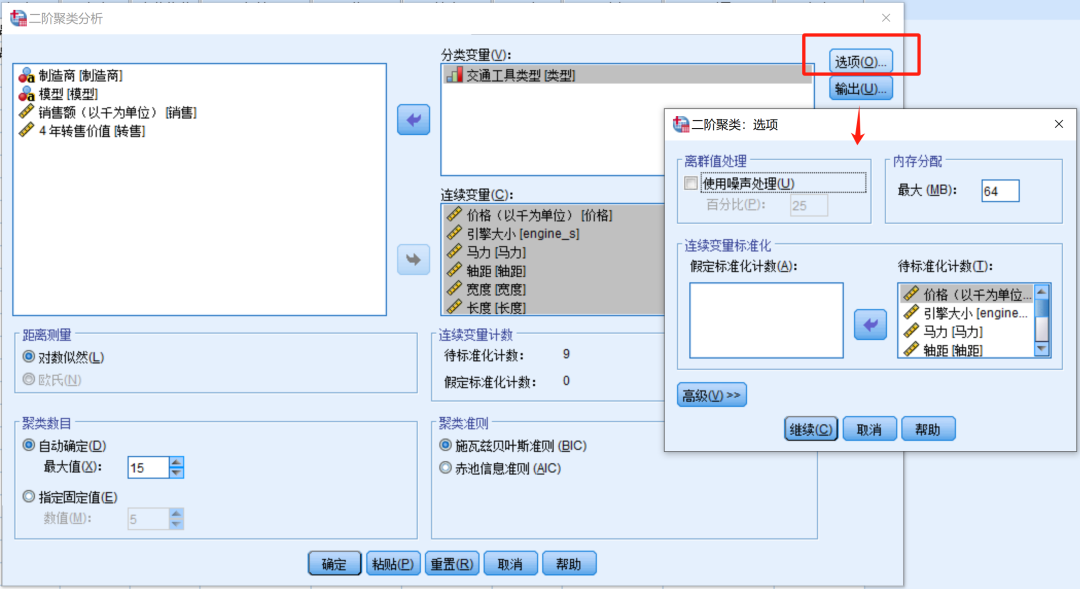
内存分配
默认。
连续变量标准化
SPSS默认对所有的数值变量进行标准化,若已进行标准化则需将待标准化计数放回到假定标准化计数内,若未进行标准化则无需进行改动。
透视表
用于展示每个聚类的描述性统计信息。当勾选此选项时,SPSS会为每个聚类生成一个透视表,表中会列出每个变量的统计描述。
图表
允许用户生成展示聚类结果的图形。这些图表可能包括散点图、条形图或箱线图等,用于可视化每个聚类在特定变量或变量组合上的分布。
表
输出每个聚类的中心点。勾选此选项后,SPSS会生成一个表格,列出每个聚类的中心点在各个变量上的值。这有助于了解每个聚类的特征,并比较不同聚类之间的差异。
创建聚类成员变量
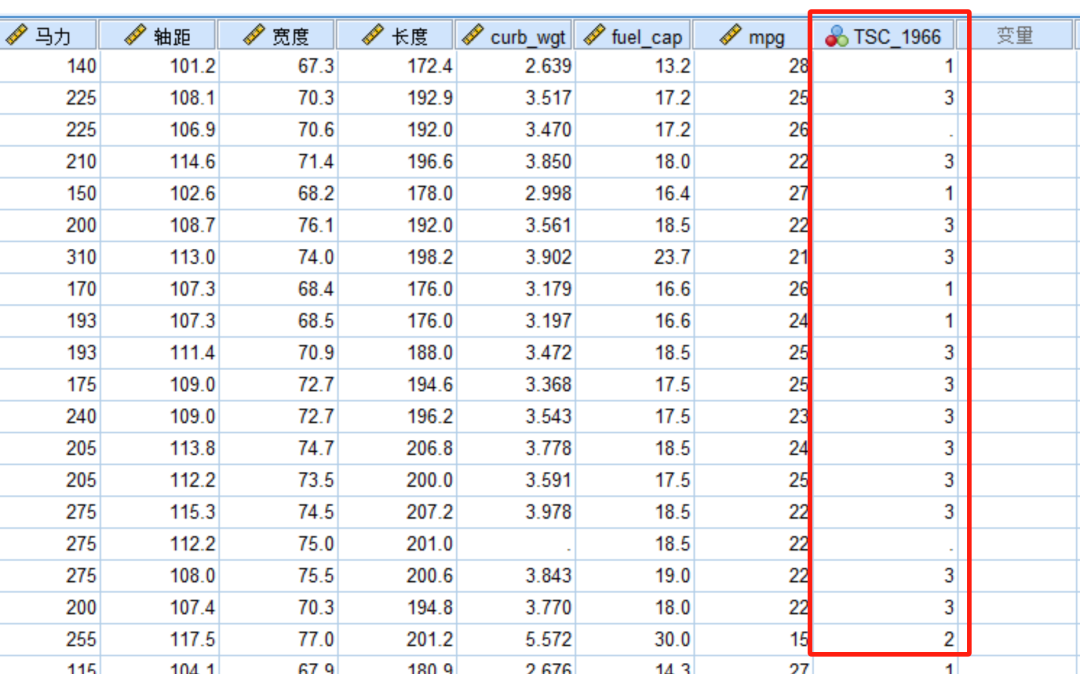
创建一个新的变量,用于标识每个观测点所属的聚类。这对于后续分析非常有用。
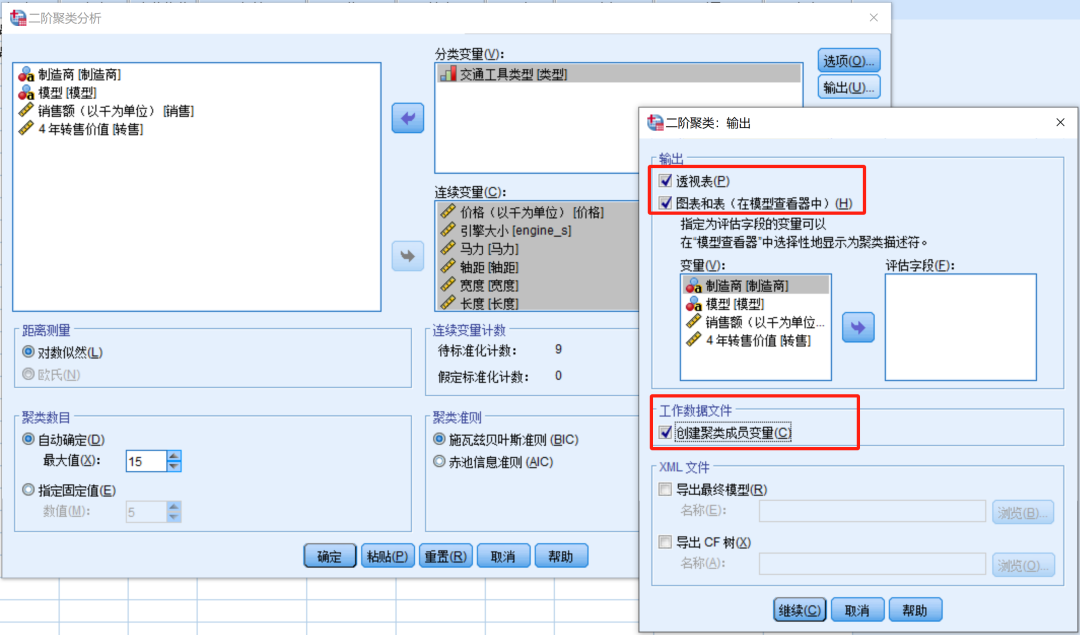
自动聚类表
用于了解软件是如何根据BIC值自动判断最终聚类个数。
SPSS软件综合四个判据,最后自动确定最佳聚类个数。
第1列表示聚类的数目。
其他4列为判断最佳聚类个数的统计量。
一般来说,在BIC统计量取较小的值+综合考虑BIC变化比率和距离测量比率最大时,模型较好。
本例中聚类个数为3类时,各统计量结果最优。
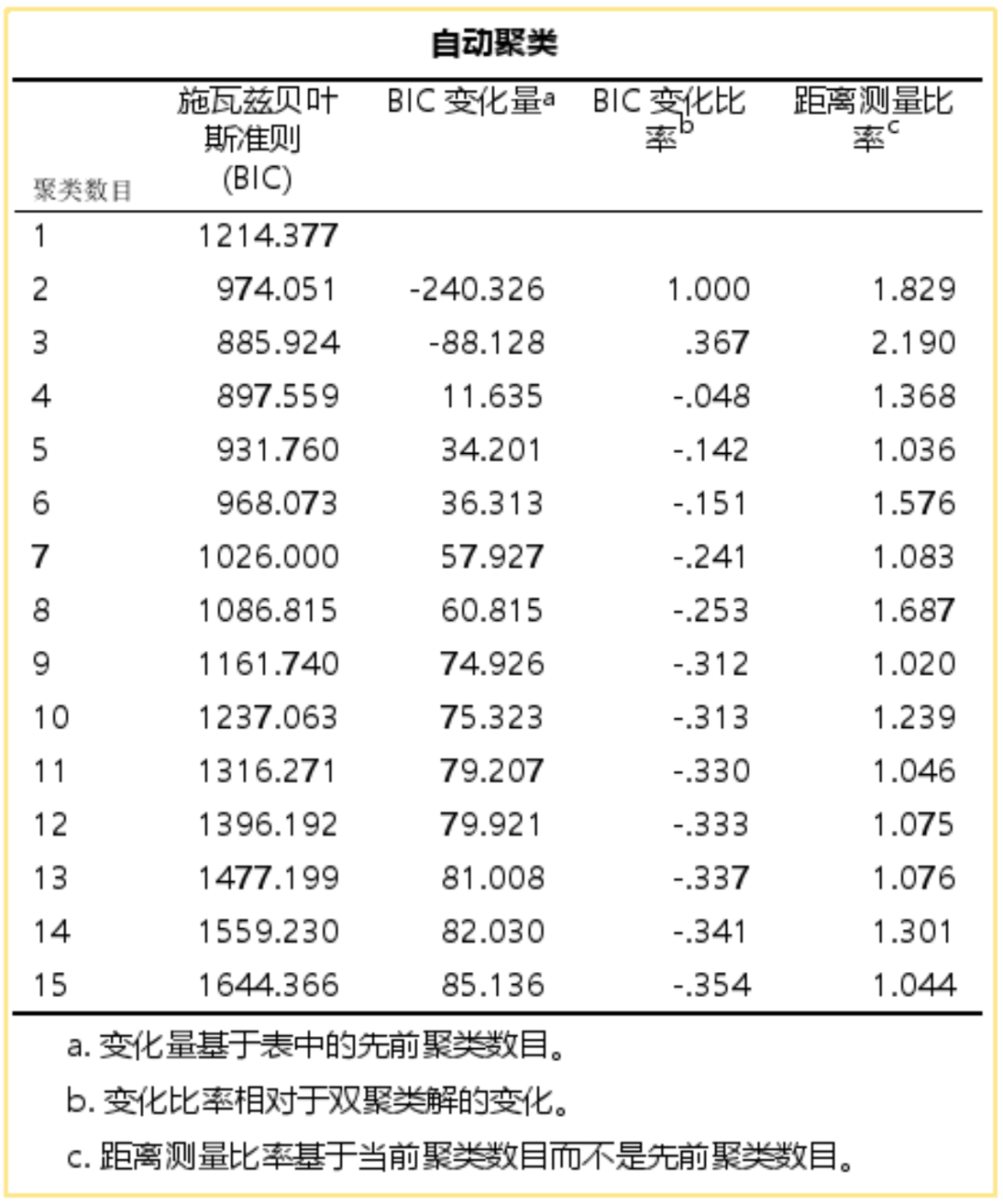
聚类分布表
描述最终聚类的描述统计分析结果。
软件给出一个3类的结果,并告知每一类的个案规模。这三类是否最合适,可以具体看类的特征是否有现实意义。
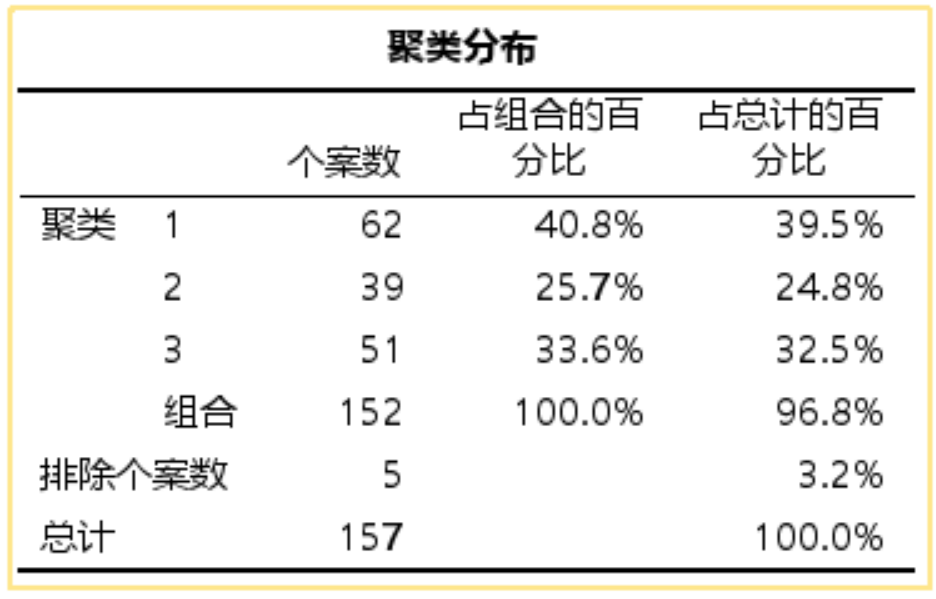
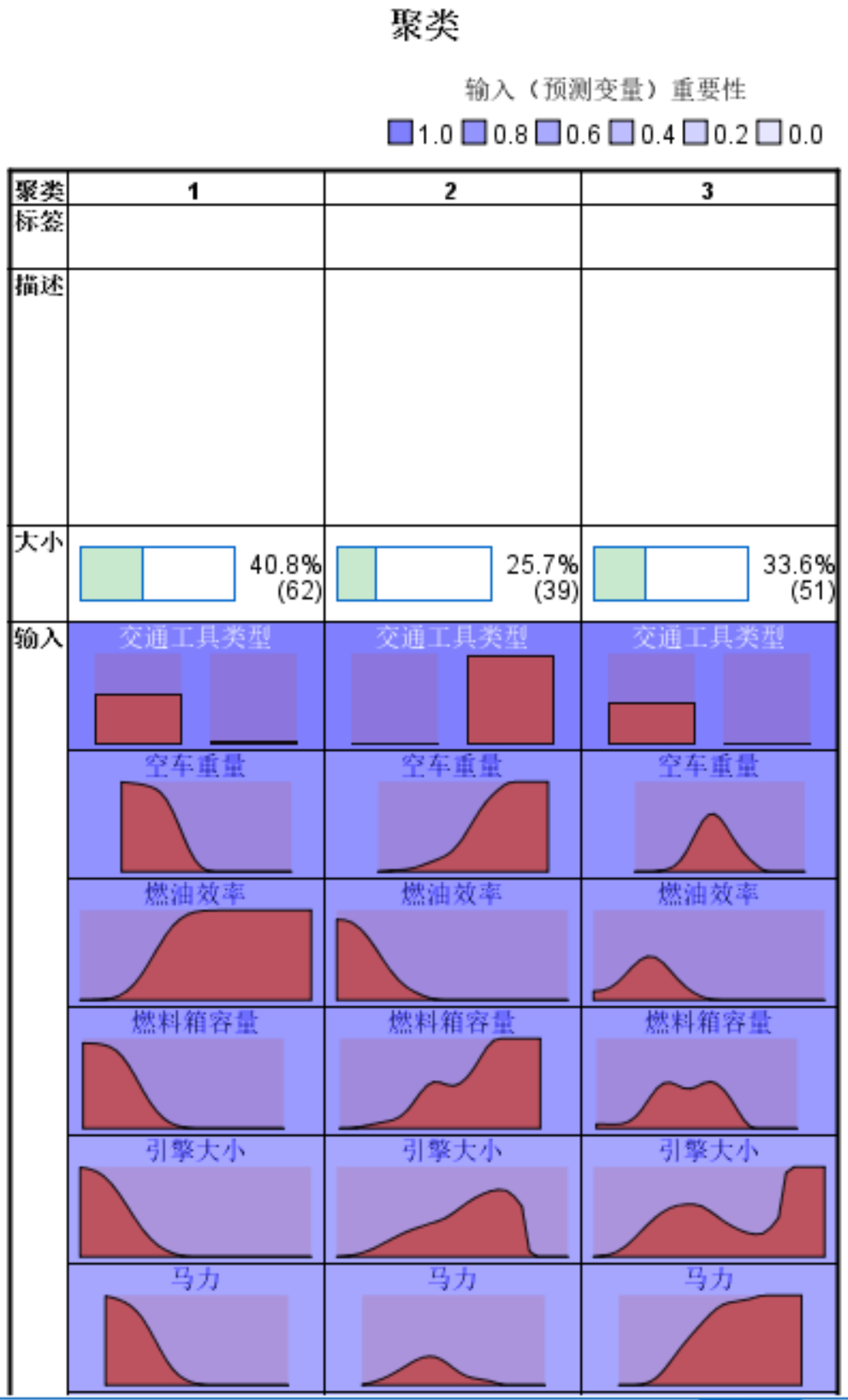
第1、3类中几乎全部为汽车,第2类中全部都是卡车。
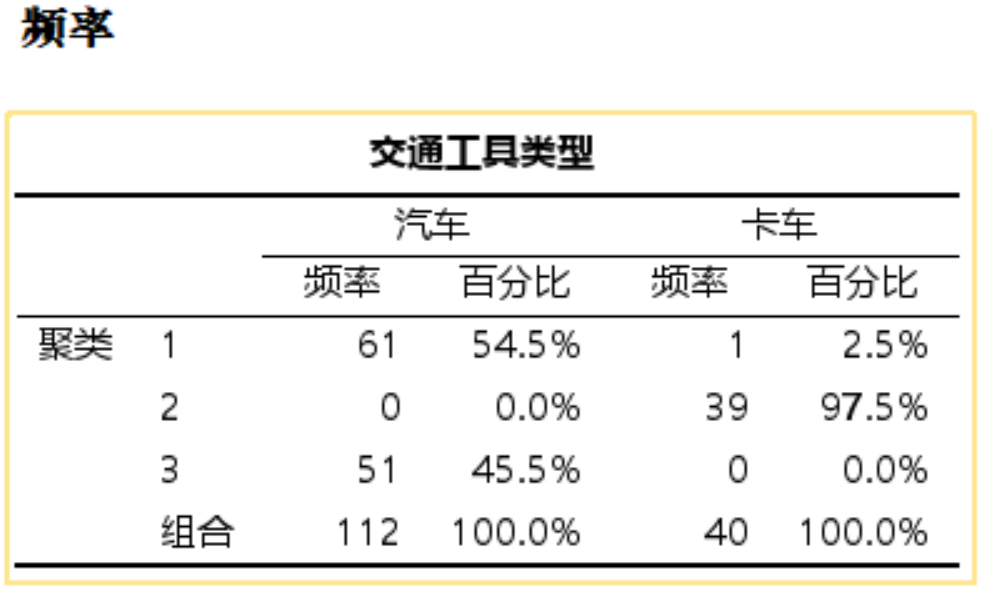
聚类概要_质心表
提供了每个聚类的中心点的详细统计信息。
质心表显示了每个聚类在各个变量上的中心或平均值,这些中心点代表了聚类内所有案例的平均特征。
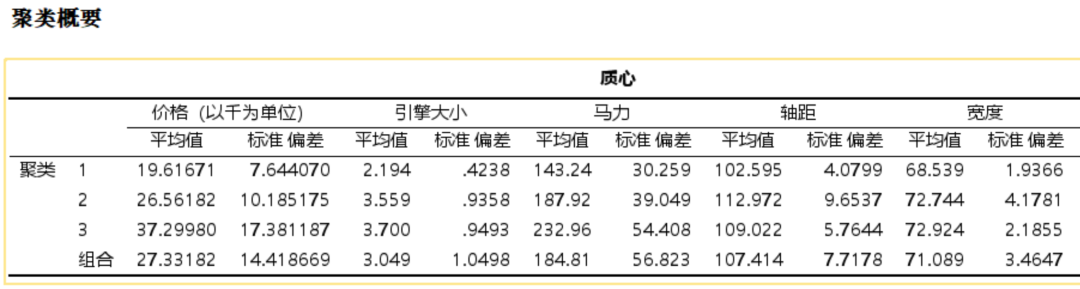
模型概要
采用两步聚类算法,自变量数为10个最终聚为3类。
总体上本次聚类质量尚能接受,还未达到良好的程度。
结果查看器中双击“模型摘要图”,打开模型浏览器,这一部分结果高度可视化,读取更直观。
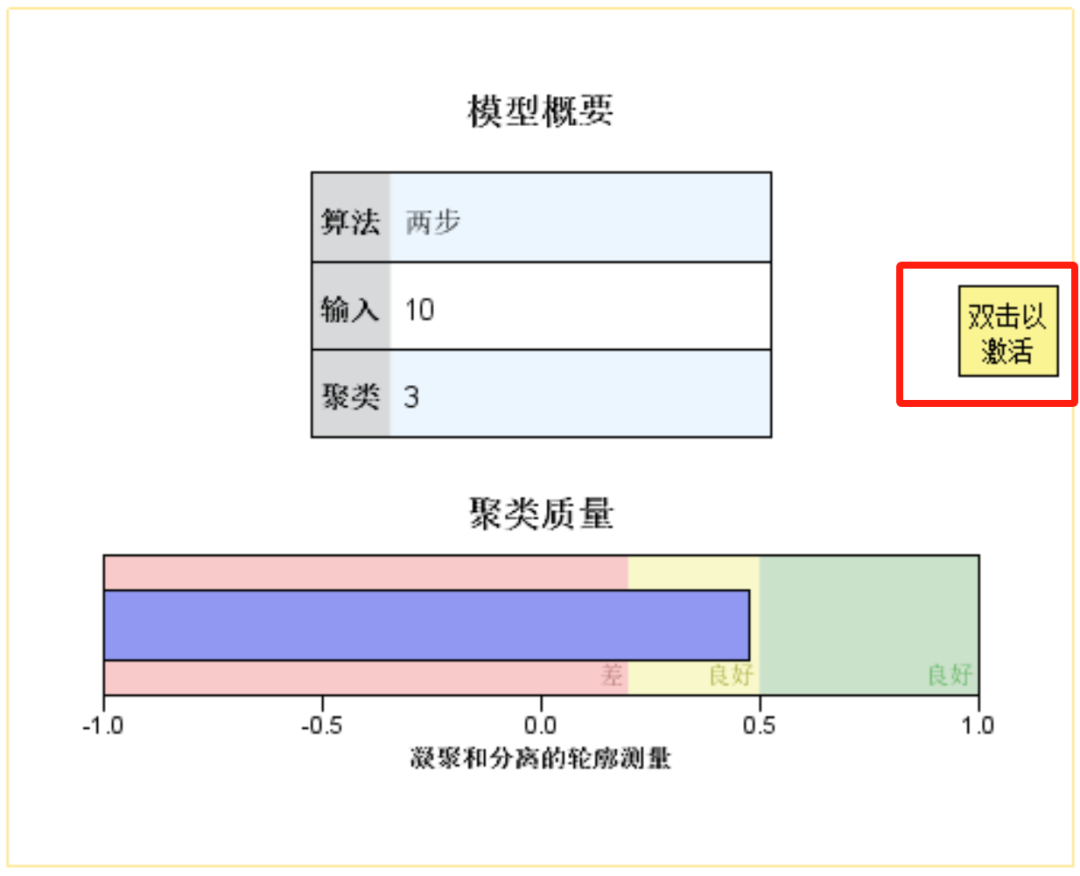
双击之后会出现这个图。
聚类大小:和前面透视表给出的结果一致。
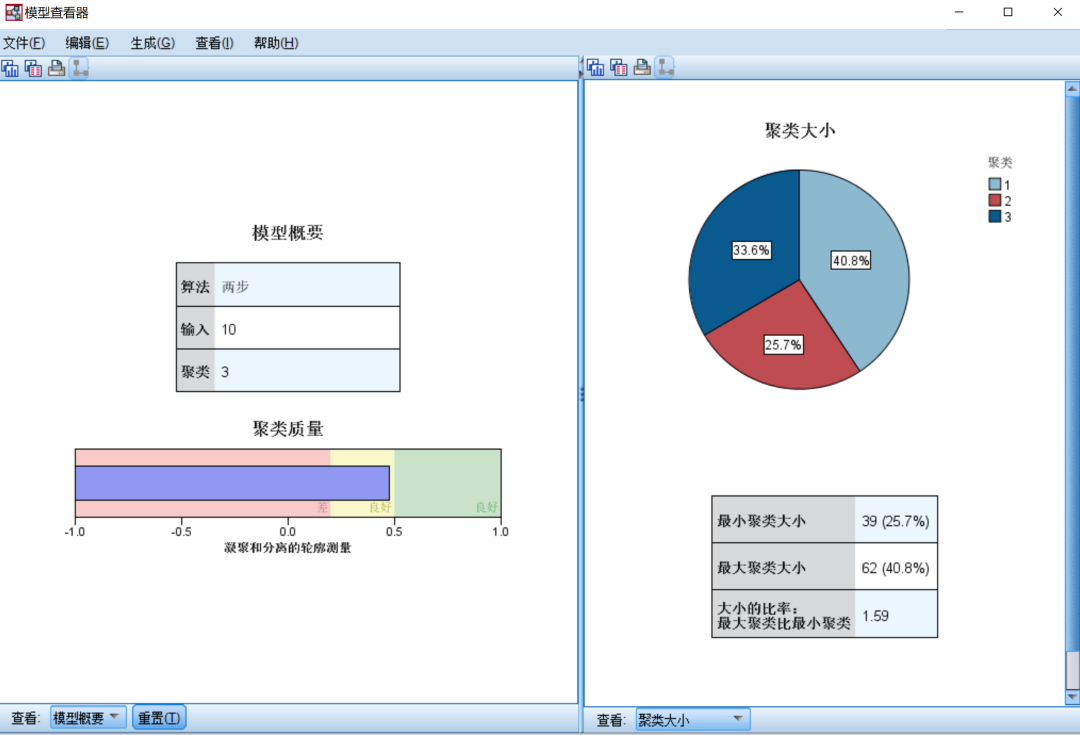
聚类
将左下的视图下拉框中将“模型概要”选为聚类,可看出这些变量分布特征以及变量在聚类分析中的重要性。
在后续中可将不重要的输入剔除再进行聚类(颜色越深越重要)。
除了颜色还可以将鼠标放在相应的模块内,会显示模型重要性&聚类中心点。
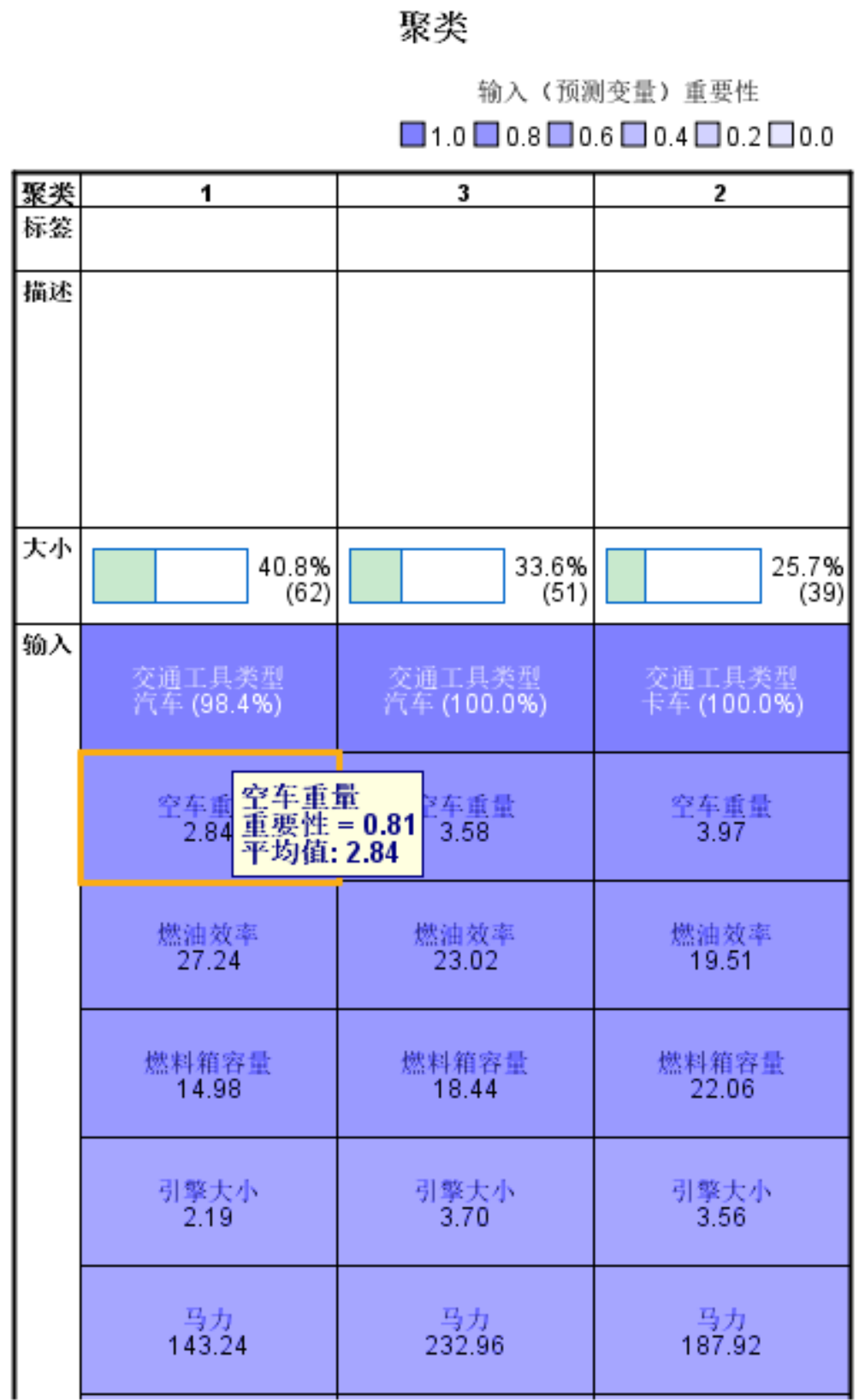
另外一种可视化方式,查看聚类结果的各个指标数据分布,分布差异越大,侧面说明该指标的重要性越高。
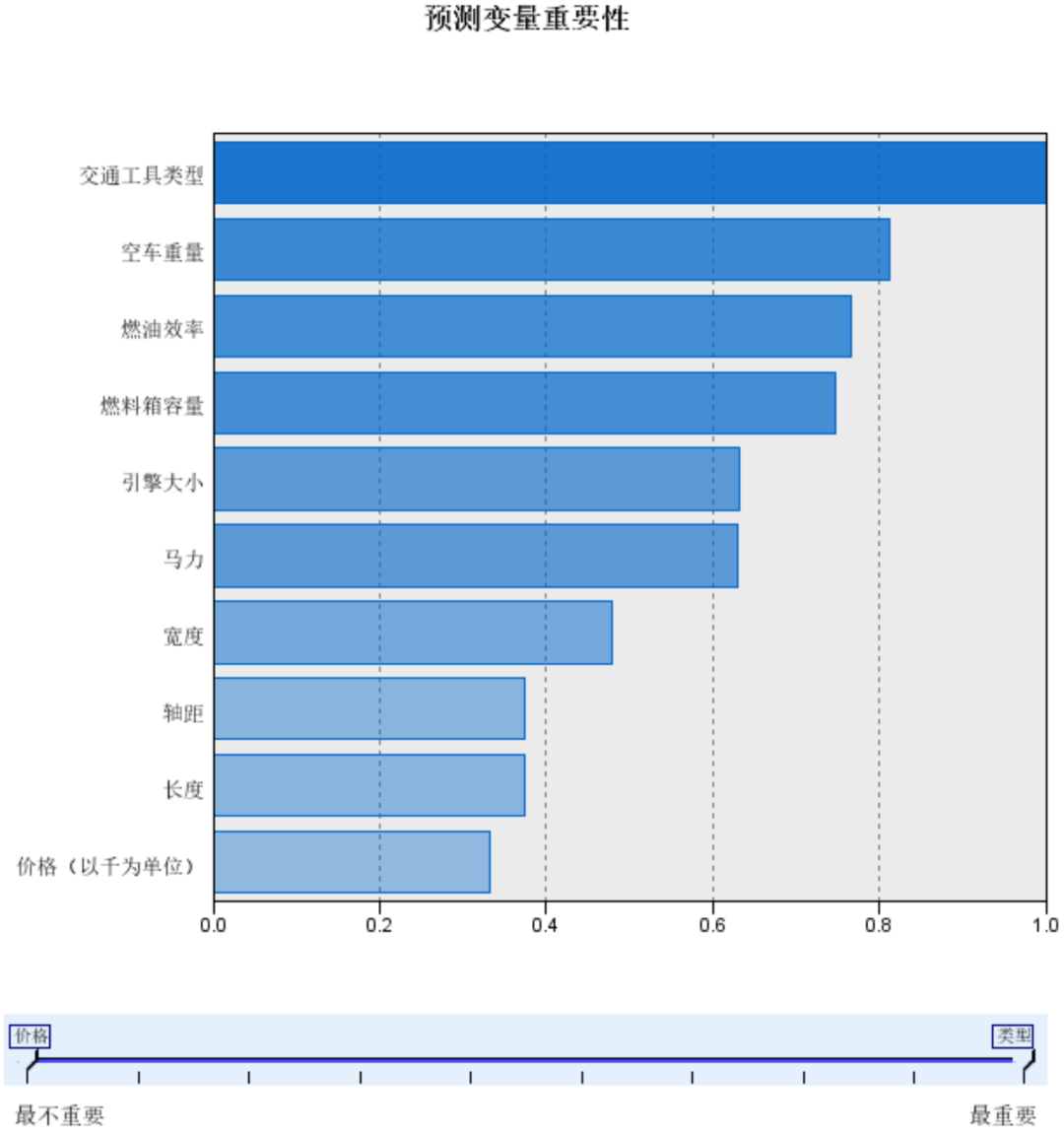
预测变量重要性:可以看到各个变量的相对重要性。
侧面也可以对变量做筛选,剔除一些重要性很小的变量,进行二次聚类分析;
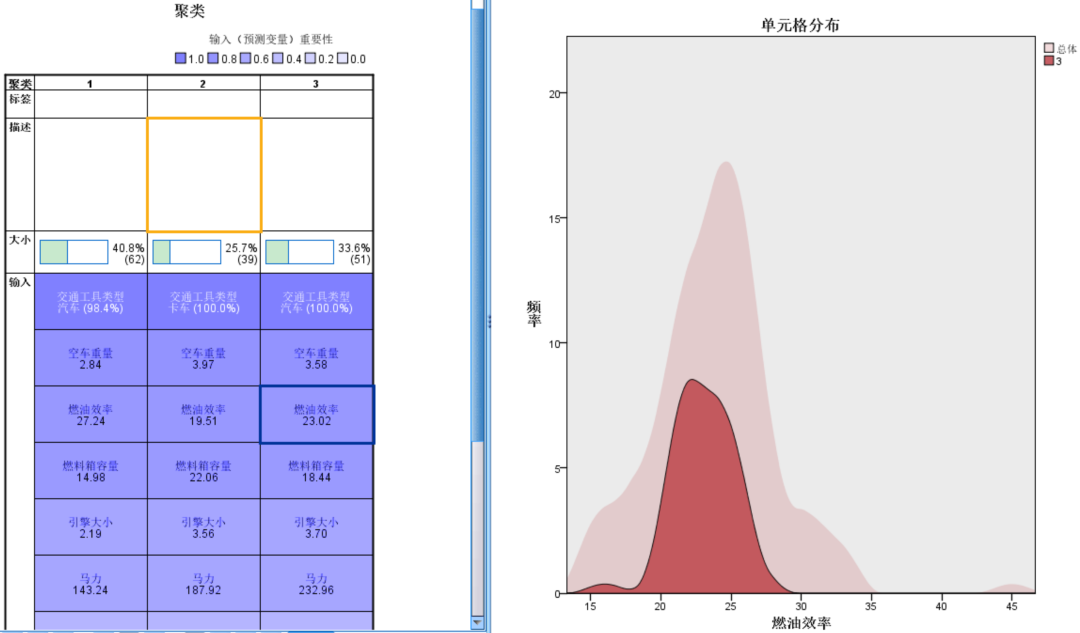
用鼠标点击图中任一单元格,右侧可以显示该变量在当前类别中的分布及该变量在总体中的分布。
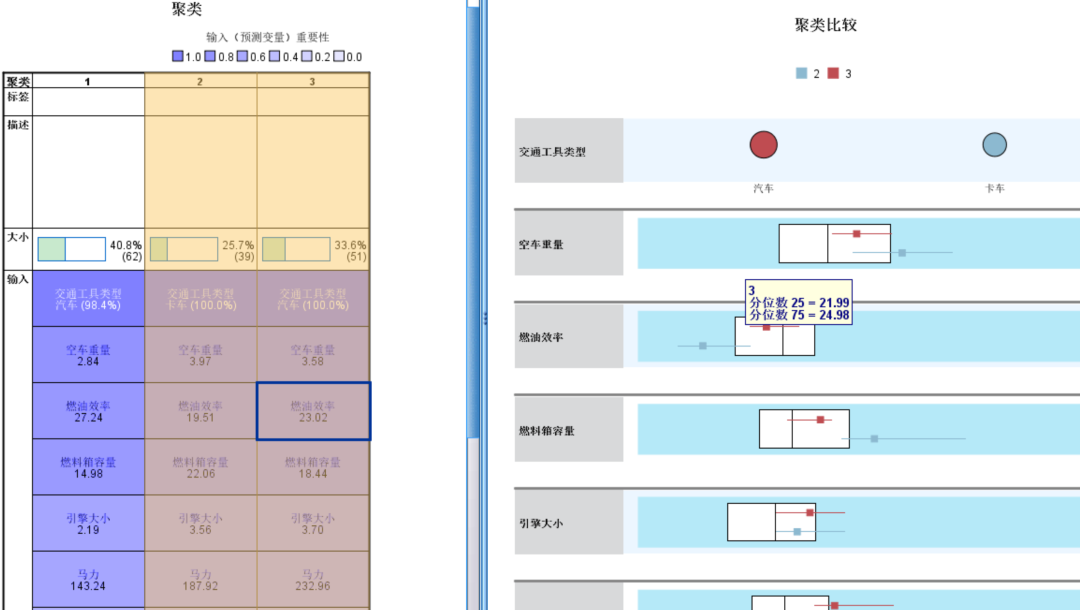
聚类比较:左侧的主视图中按ctrl键,同时选定两个或以上类,在右侧视图中将出现两个类或以上类的特征对比。
鼠标放在右图线上可以看到不同聚类结果&总体的25分位数、中位数和75分位数。
聚类判别
判别每行数据所属的类别。
软件将其自动保存在数据视图最后一列,新生成变量“TSC_n”,其中TSC即表示二阶聚类,n是一个正整数,表示的是类内平方和的总和,即所有聚类内部数据点与各自聚类质心之间差异的平方和。
TSC是评估聚类效果的一个重要指标,它衡量的是聚类内数据的紧密程度。数值越小,表示聚类内部的数据点越接近其质心,即聚类效果越好,数据点在各个变量上的一致性越高。
聚类分析是一种探索性方法(会存在聚不出好结果的情况),更像是一种建立假设的方法,严谨分析的话还需要借助其他方法对于这种分类进行检验。
主要运用方差分析等方法来进行检验,即验证具体分类类别在N个维度上的均值是否有差异。