 基础聚类方法_K-means聚类
基础聚类方法_K-means聚类基础认识
K-means聚类是一种常用的无监督学习算法。
是划分聚类(快速聚类)的一种,英文名称K-means Cluster。
是一种常见的聚类算法。
是一种基于距离度量的聚类算法。
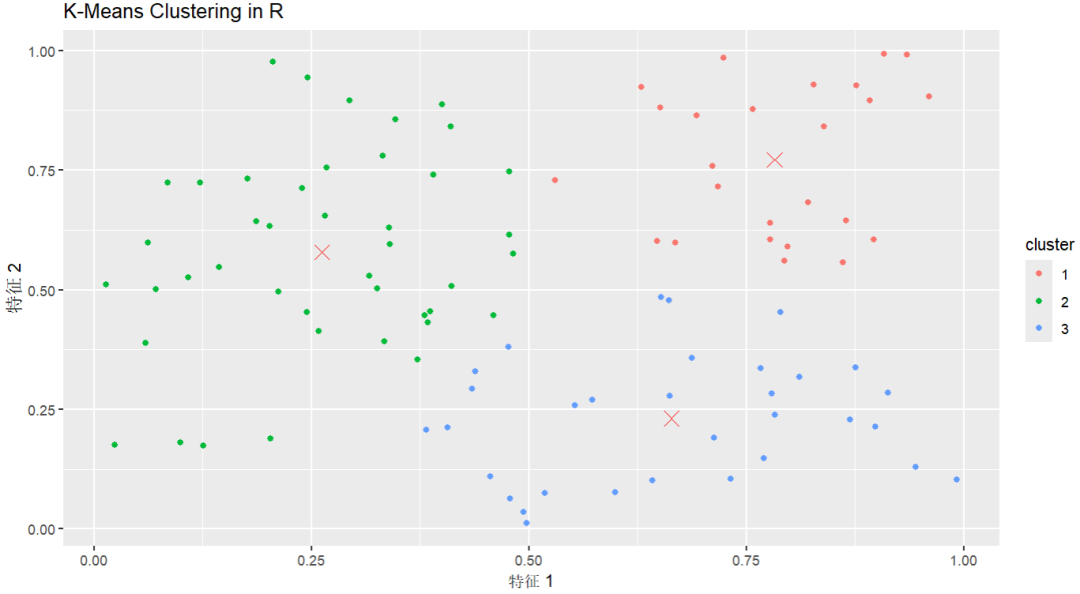 (图例仅作示意)
(图例仅作示意)原理
将数据集中的样本分成 K 个不同的组或簇。
通过在数据集中的样本之间计算距离(欧氏距离)来确定簇的中心,并将每个样本分配到离其最近的簇。
这个过程不断迭代,直到簇的中心不再发生显著变化或达到预定的迭代次数。
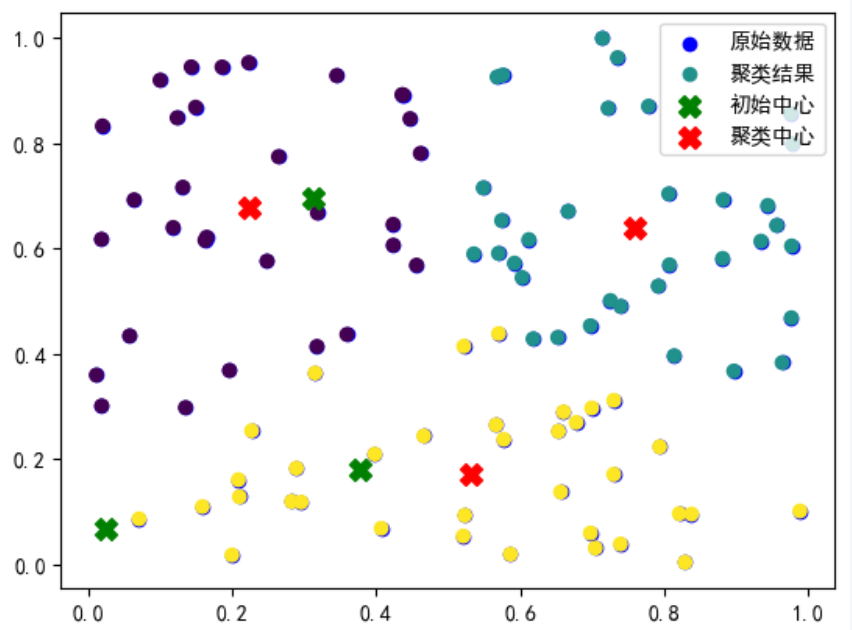 (图例仅作示意)
(图例仅作示意)计算步骤
- 初始化K个簇中心(通常是随机选择K个数据点)。
- 计算每个数据点到所有簇中心的距离,并将其分配到最近的簇。
- 更新每个簇的中心为当前簇中所有数据点的均值。
- 重复步骤2和3,直到簇中心不再发生显著变化或达到最大迭代次数。
优势
- 简单高效:易于理解和实现。
- 计算效率高:时间复杂度为O(nkt),适合处理大规模数据。
- 适用于均衡簇数据:当数据集的簇是相对均衡,且各簇的形状类似球状时,表现较好。
- 对高维数据有效:K-Means 在处理高维数据时相对有效,尤其是当簇的维度(≈变量的分类特征)相对较低时。
劣势
- 对初始簇中心敏感:不同初始簇中心可能导致不同聚类结果,结果可能只是局部最优,非全局最优。
- 对噪声敏感:少量离群点和噪声点对算法求平均值产生极大影响,聚类结果会受到干扰。
- 需要指定簇的数量K:对于某些数据集而言可能是不客观的,K的取值影响最终聚类结果。
- 对非球形簇效果差:算法假设簇具有球形结构,当数据集中的簇形状不是球状时,表现可能较差。
- 对簇大小差异大的效果差:K-Means对大簇的处理可能更好,对小簇的处理可能较差。
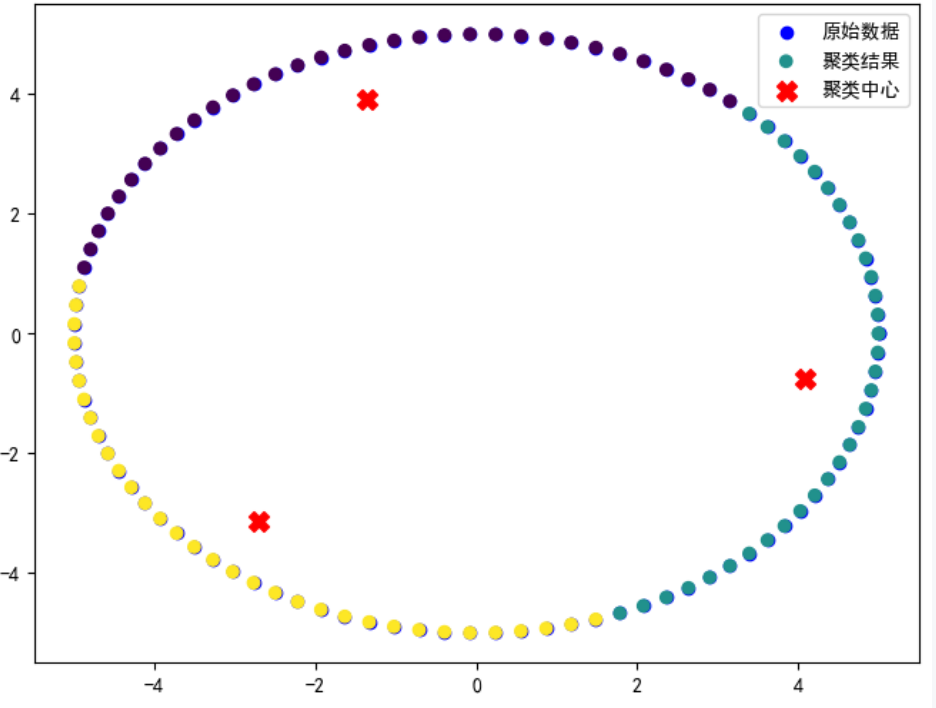 (图例仅作示意)
(图例仅作示意)前提条件
- 必须是连续型数值(若是离散变量,需作哑变量处理)。
- 数据作标准化处理(防止不同量纲&数据量级差异大而对聚类产生影响)。
- 数据集不含显著的异常值:异常值会导致不准确的聚类结果。
- 需要预先确定簇的数量K:K-means要求事先确定簇的数量。
- 更适合于球形or凸形状的簇,因为是基于距离度量来计算簇之间的相似性。
- 变量之间不应有较强的线性相关关系,避免计算距离时这些变量将重复贡献,影响最终聚类结果。(可进行批量相关性检验)
实现工具
- Python库:如Scikit-learn。
- R语言包:如cluster。
- MATLAB工具箱:如Statistics and Machine Learning Toolbox。
- 数据分析软件:如SAS、SPSS等。
Rj语言实践
仅做简述,具体需要上手敲代码,实现聚类会更灵活。假设K=2,分为两类。
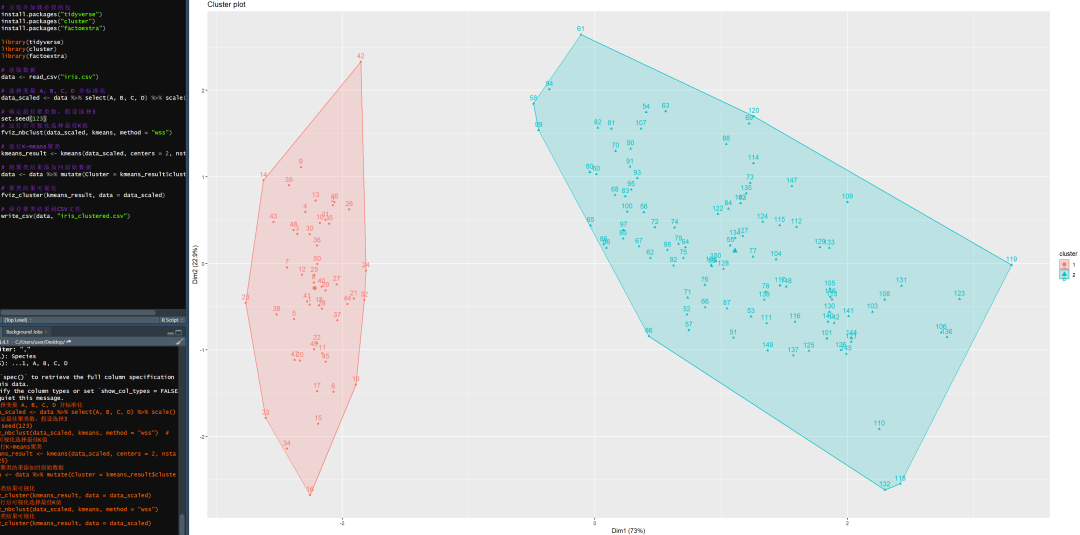 (通过cluster包实现K-means聚类,整体聚类效果良好)
(通过cluster包实现K-means聚类,整体聚类效果良好)检验聚类数是否合适,采用肘部法则,K=2时直线倾斜程度最高,聚为2类效果更好。
详细关于如何确定聚类数的方法,后续文章会进行完整描述。
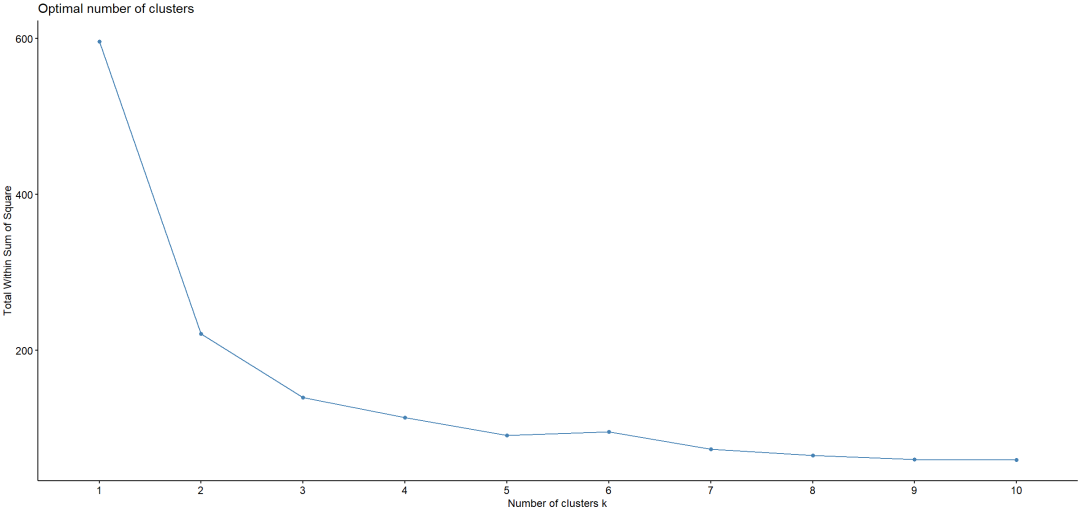 (使用肘部法则来验证最佳聚类数,fviz_nbclust 函数可帮助可视化选择过程)
(使用肘部法则来验证最佳聚类数,fviz_nbclust 函数可帮助可视化选择过程)SPSS实践
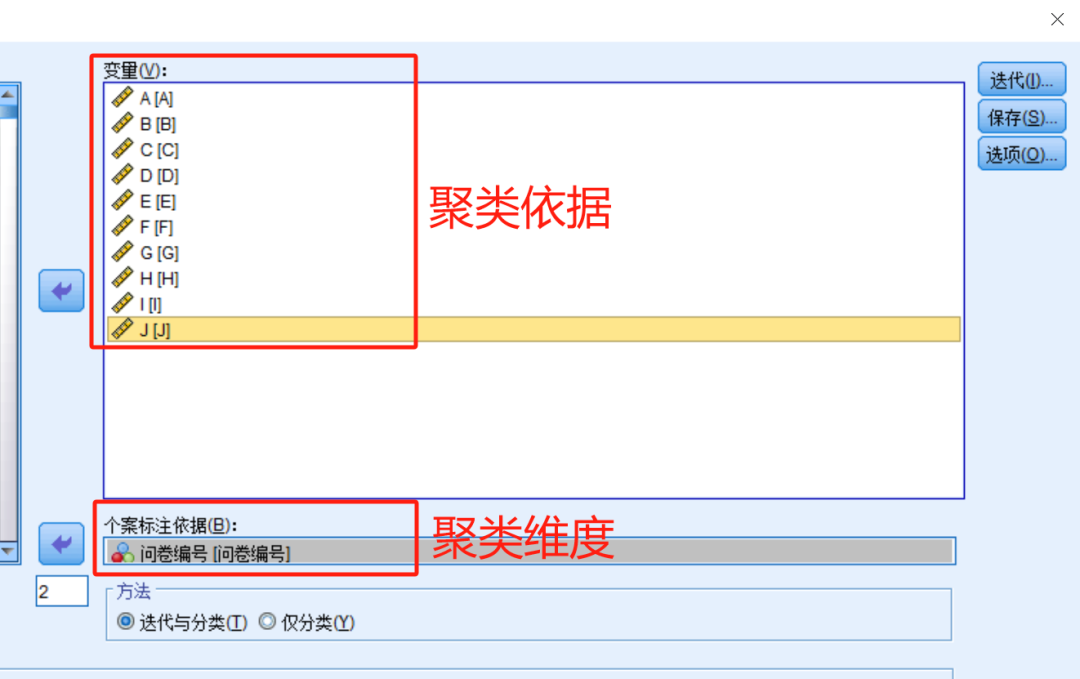
分析—分类—K均值聚类
- 变量 :聚类的依据;
- 个案标注依据 :最终聚类的点以何种维度表示;
聚类数目需要自行设定,可多轮测试尝试,但一般不宜过多;
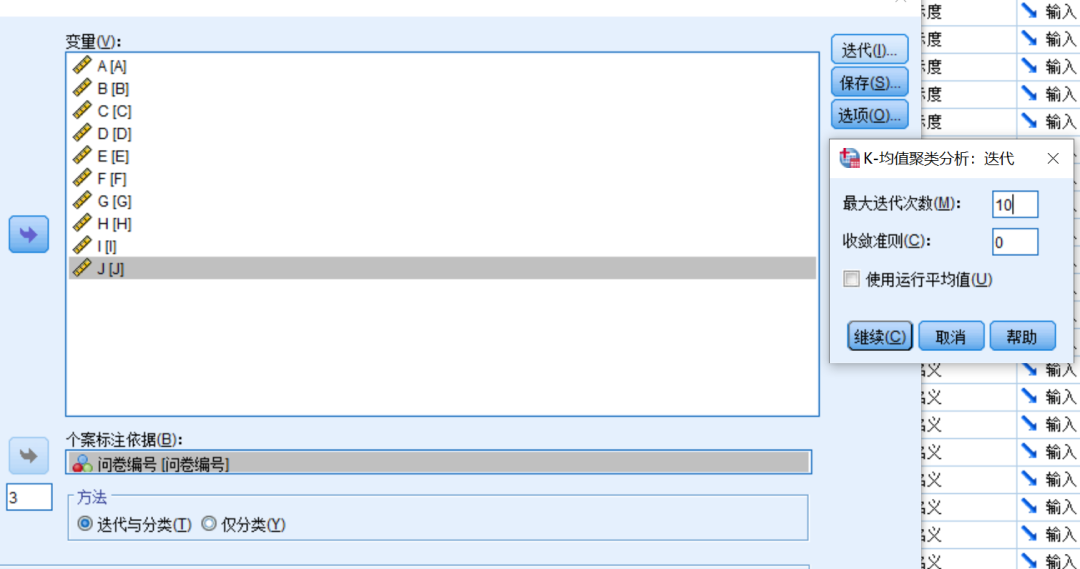
 迭代:系统默认最大迭代次数为10,收敛标准为0;
迭代:系统默认最大迭代次数为10,收敛标准为0;即前后2次如果各点到聚类中心的距离之差为0,则达到收敛标准,即已找到最佳聚类中心,可以进行聚类。
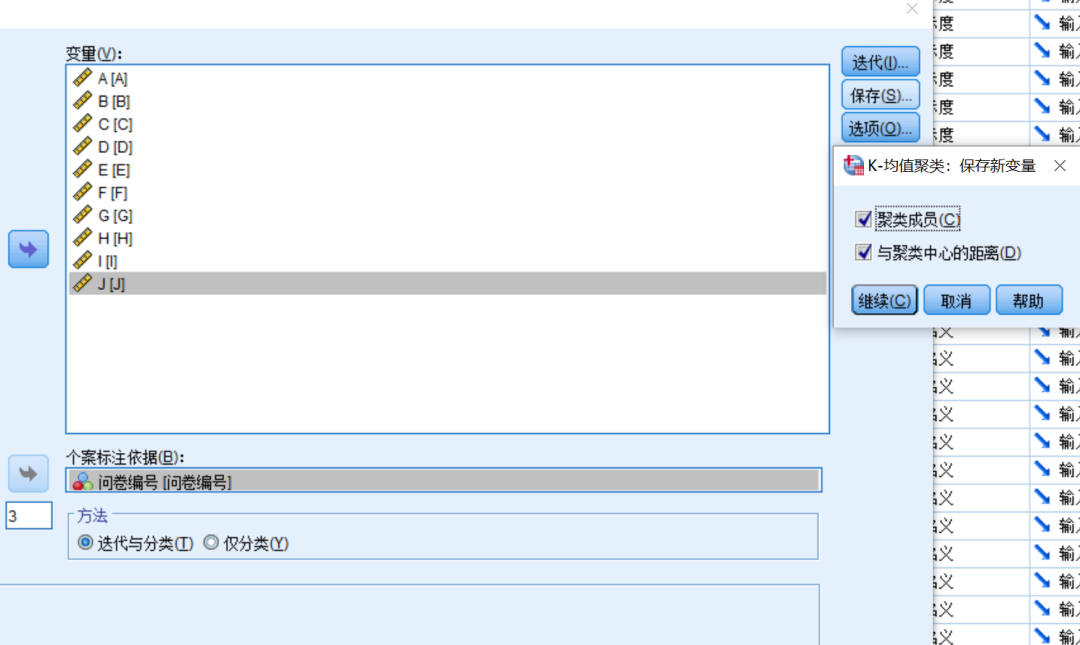
- 保存:勾选“聚类成员”和“与聚类中心的距离”;
- 选项:勾选“初始聚类中心”和“ANOVA表”;
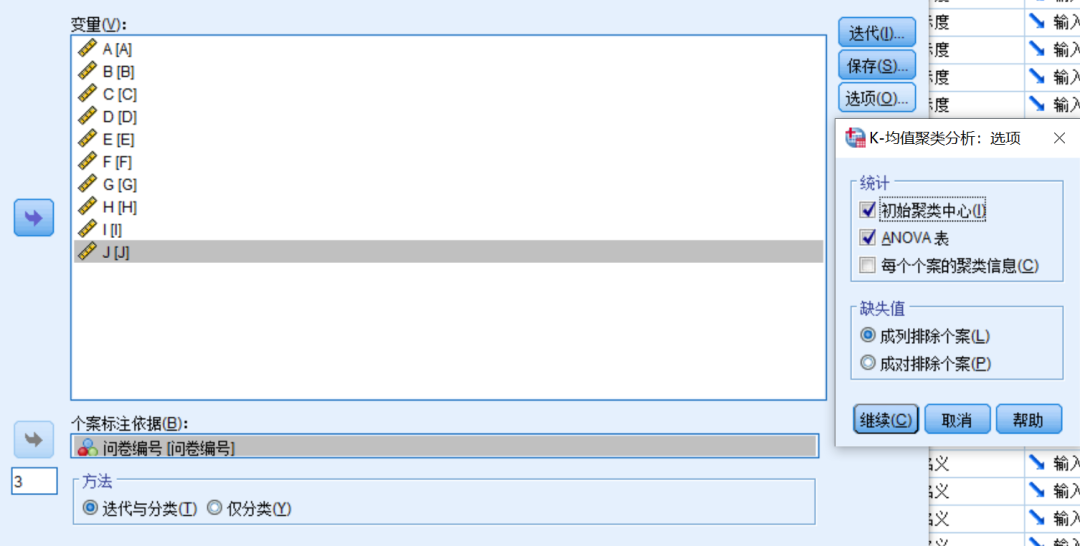
结果解读
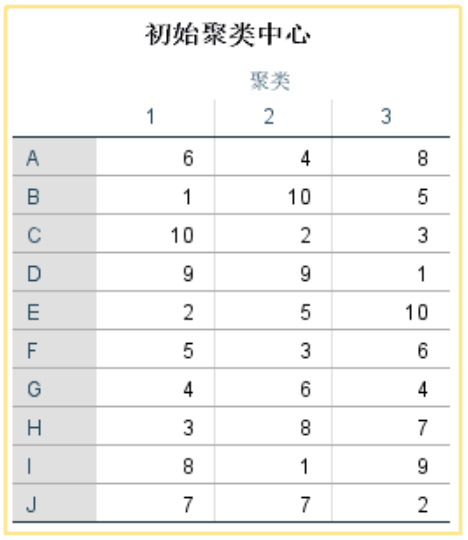
初始中心为计算机随机产生,对结果判读意义不大。
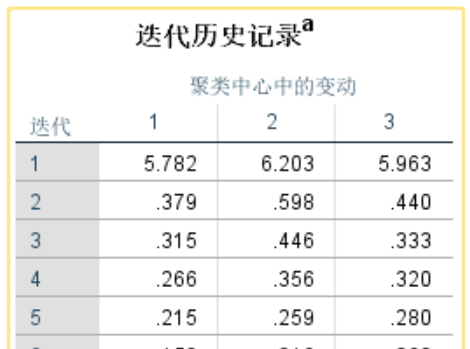
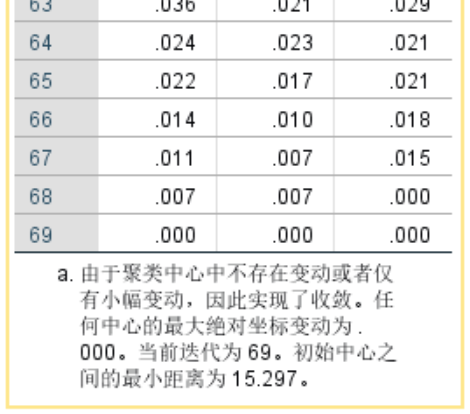
迭代记录显示69次迭代,3个聚类中心均达到收敛标准0;
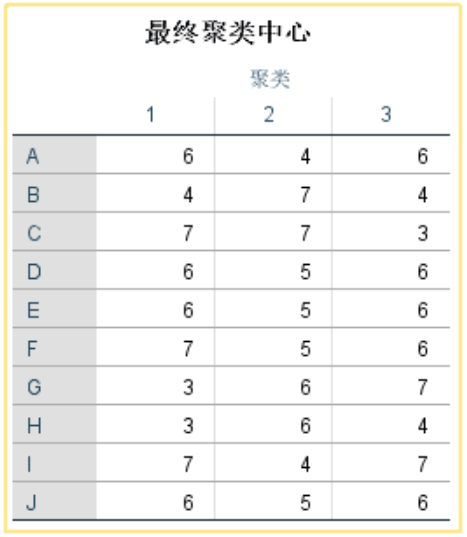
最终聚类中心,是各个类的均值,如果最终聚类可接受,则这个类中心可保留,用于以后聚类。
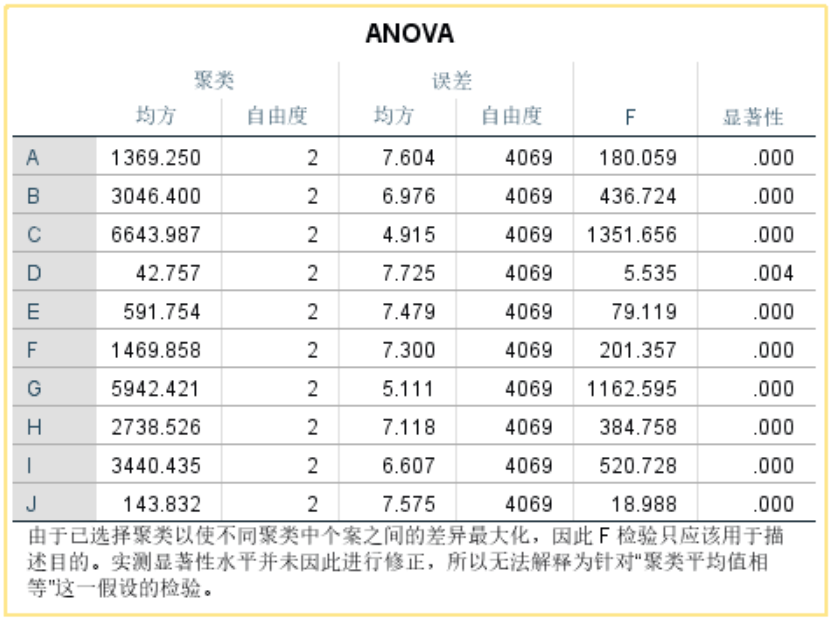
ANOVA表:对各变量均进行了方差分析,P均小于0.05说明全部变量对聚类结果均发挥作用。
F值:值越大,该值对应的变量在聚类分析中的影响更大。
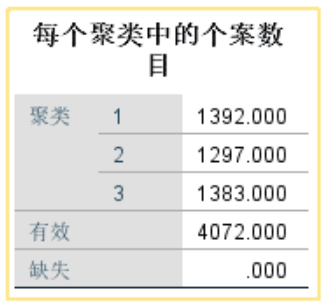
聚类个案数目:可见1类有1392个,2类有1297个,3类有1383个。
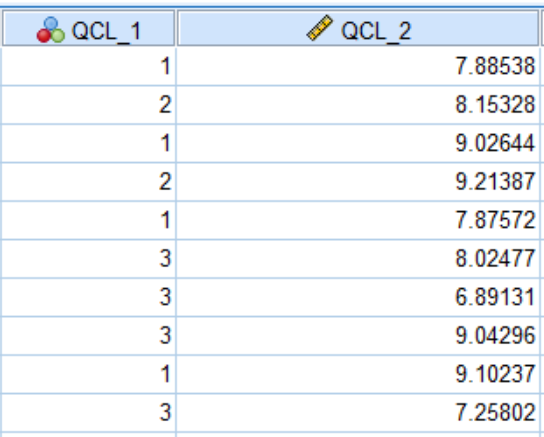
另外,将结果保存为新变量。在变量视图里已经生成QCL_1,表示第一轮聚类结果。

 注:spss并没有给出有效的分析图表。这里需要分析者自己寻找合适的图表来有效表达各类特征。
注:spss并没有给出有效的分析图表。这里需要分析者自己寻找合适的图表来有效表达各类特征。可考虑采用SPSS中的散点图来进行可视化操作。
应用场景
- 市场细分:根据用户行为、消费习惯等进行市场细分。
- 图像压缩:通过减少颜色数来压缩图像数据。
- 文本分类:将文档分成不同的类别,以便于信息检索和管理。
- 生物信息学:分析基因表达数据,识别基因功能的相似性。
拓展延伸
关于k-means聚类的家族。
- k-medoids算法:对异常值不那么敏感,因为它使用的是实际的数据点:选择簇中的一个实际数据点作为中心点(而非均值)
- k-medians算法:每个簇的中心点是其成员数据点在每个维度上的中位数(而非均值)。这种方法同样减少了异常值的影响。
- k-modes聚类:专门用于处理分类数据(名义数据)。
- Kernel K-means聚类:将数据映射到高维空间进行聚类,适用于处理非线性分布的数据(非凸聚类)。
- K-means++聚类:改进初始中心选择方法,减少聚类结果对初始值的敏感性。
- Mini-Batch K-means聚类:适用于大规模数据,通过使用小批量数据进行迭代,降低计算复杂度。
- Fuzzy C-means聚类:每个数据点属于多个簇,适用于数据点存在模糊边界的情况。
- Bisecting K-means聚类:一种层次化的K-means变体,通过逐步二分数据集进行聚类。
END

















