基础认识

DBSCAN（Density-Based Spatial Clustering of Applications with Noise）作为一种基于密度的聚类算法，尤其适用于识别用户群体间的自然分层和潜在细分市场。

它能够有效处理任意形状的数据分布和噪声数据。

原理

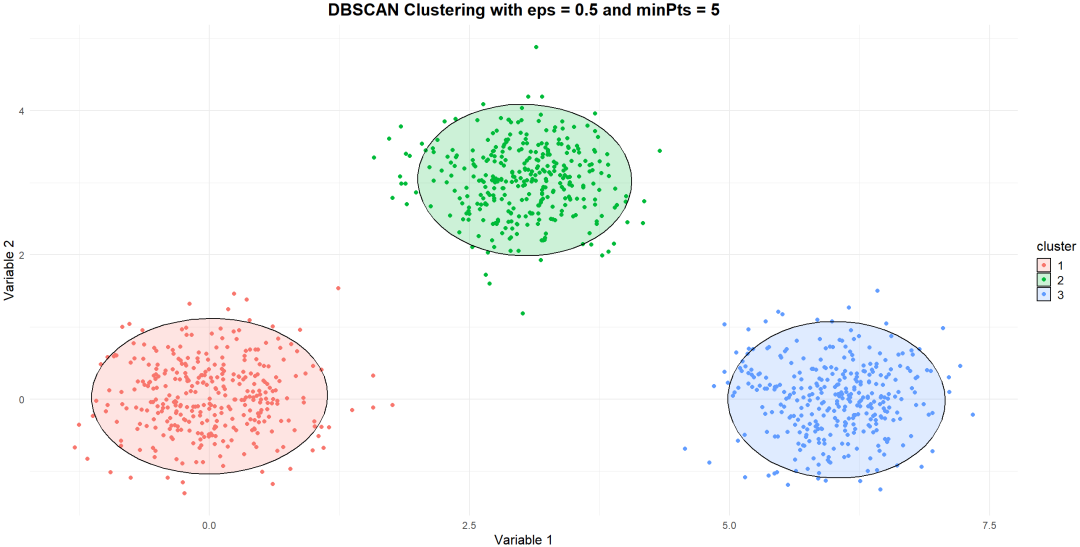
该算法的核心思想是将具有高密度的区域划分为簇，去除噪声。

如何定义高密度？

1. 定义两个参数： ε（邻域半径）和MinPts（最小邻域点数）。
2. 把数据点分为三类：核心点、边界点和噪声点。

ε（邻域半径）: 半径参数，用来定义邻域的大小，即一个点如果在其半径ε范围内存在足够数量的邻居点，则被认为是高密度区域的一部分。

MinPts（最小邻域点数）: 表示在一个点周围 ε 范围内的最少点数，只有当这个点的邻域内点数超过 MinPts 才会被认为是核心点。

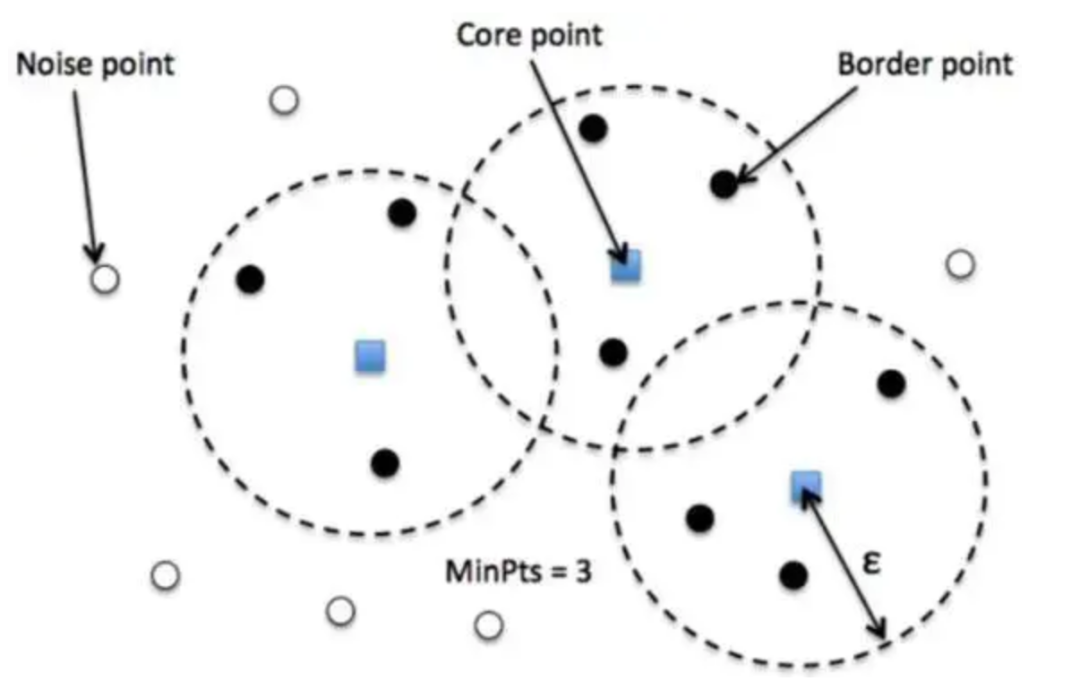
核心点：在一定半径内（Eps）有足够多（最小点数MinPts）邻居的点；

边界点：在其邻域内少于MinPts个点，但落在某个核心点的邻域内的点；

噪声点：既不是核心点也不是边界点的点。

前提条件

1. 数据应具有有意义的密度差异，以便区分不同的簇。
2. 数据应该是数值型，因为算法基于距离度量进行聚类。
3. 数据标准化处理，以消除不同量纲带来的影响。
4. 需要合理设定Eps（邻域半径）和MinPts（最小点数）的值。
5. 需要定义一个合适的距离度量方法。

实施步骤

1. 初始化：遍历数据集，计算每个点的邻域密度。
2. 核心点识别：标记邻域密度高于阈值（即满足MinPts条件）的点为核心点。
3. 构建聚类：利用核心点扩展簇，将核心点的邻域内其他核心点和边界点归入同一簇。
4. 全部标记：继续拓展直至整个数据集的所有点都被分配到相应的簇或标记为噪声点。

优势

1. 自动识别簇的数量，无需预设聚类个数。
2. 对于任意形状的簇表现良好（包括凸形、凹形以及不规则形状）。
3. 能够发现并标识噪声点（鲁棒性），这对排除异常值非常有用。

劣势

1. 参数敏感性：ε和MinPts的选择至关重要，选择不当可能导致过拟合或欠拟合。
2. 密度要求：在簇的密度差异过大or过度均匀or过度稀疏时，无法有效区分，聚类效果可能不理想。
3. 高维数据：随着维度增加，局部密度估计变得困难，选择合适的ε更加不易（可考虑降维）。

新的算法正在被提出来，比如OPTICS。

代码实现

Python：scikit-learn库

R：fpc包（包含了dbscan包）

以下以R为例进行分析，数据为SPSS软件自带数据集。

注意事项

如何合理设定Eps（邻域半径）和MinPts（最小点数）？

可视化探索

1. 二维散点图：绘制数据的散点图来观察数据分布情况，从图中可以大致估计出合适的Eps值。
2. 直方图：绘制数据点间距离的直方图，寻找距离分布的显著断点或陡峭变化处，这些位置可能有合适的Eps值。
3. K-distance图：绘制每个点的 k 距离（即距离该点最近的第 k 个点的距离）随 k 增长的曲线。曲线的拐点或平缓区通常对应合理的Eps值，因为这些位置标志着邻域点数量显著增加或减少。

以K-distance图为探索示例

解读：通常选择肘部位置对应的 K-distance 值作为EPS，并根据初始斜率来调整MinPts（较大的斜率可能意味着选择较小的MinPts 值；而较小的斜率则可能需要较大的MinPts 值）。

① 局部密度变化：K-distance 反映了数据点的局部密度。当 K-distance 较小时，意味着数据点附近有较多的邻近数据点，密度较高；而当 K-distance 较大时，意味着数据点附近的邻近数据点较少，密度较低。

② 肘部位置：K-distance 图的“肘部”通常对应着数据集的自然分界点。在肘部附近，K-distance 的变化率会明显减小，表示数据集中存在一个相对明显的密度变化点，可以作为选择 EPS 参数的依据。

③ 密度变化趋势：观察 K-distance 图的整体趋势，可以了解数据集的全局密度分布情况。当 K-distance 图整体上呈现出递增或递减趋势时，可以推断数据集的密度分布特征。

④ 异常点识别：K-distance 图还可以用于识别异常点。通常情况下，异常点的 K-distance 值会较大，因为它们可能远离其他数据点或处于低密度区域。

数据特性

① 如果数据点分布比较密集，Eps应该设定得较小，以便捕捉到更精细的聚类结构。

② 如果数据点分布比较稀疏，Eps应该设定得较大，以避免将单个数据点误判为噪声。

启发式方法&基于领域知识

如果有关于数据分布的先验知识或者业务经验，可以利用这些信息来设定参数。他们不是基于严格的数学证明，而是基于以往的经验、直觉或是一些简单的规则，它们往往能够提供解决问题的有效途径。

调整试错法

① 尝试不同的参数组合：先设定一组初始参数，根据初步聚类结果，观察簇的连贯性和噪声点的分布情况，逐步调整 Eps 和 MinPts ，直至得到满意的结果。

② 网格搜索：设定一个 Eps 和 MinPts 的取值范围，通过网格搜索的方式遍历不同的组合，对每组参数运行DBSCAN，评估聚类效果（如轮廓系数、Calinski-Harabasz指数等），选择最优参数组合。

轮廓系数是一种衡量聚类结果质量的指标，可以帮助确定最佳的聚类参数。尝试不同的参数组合，并计算每个聚类结果的轮廓系数，选择使轮廓系数最大化的参数组合。

其他聚类算法

① 使用如OPTICS算法生成的可达图，它不需要预设 Eps 和 MinPts ，可以推导出适用于DBSCAN的参数。

另外有文章会专门写这个聚类算法。

② DBSCAN的变体，如HDBSCAN，对参数选择不那么敏感，能够自适应地确定eps值。

HDBSCAN并不直接在CRAN上提供，只能通过其他途径在R中安装，最常见的是从GitHub上安装。需要提前安装了devtools包，但我操作后还是失败了，具体原因不详。

市场应用

客户细分

如根据购买频率、平均消费额、购买的商品种类等特征，将顾客划分为不同的细分市场。用于理解需求，定制营销策略。

地理位置分析

如结合地理坐标信息，发现高密度的商业热点区域或消费者活动集中区域。

异常检测

通过市场数据中的异常值和离群点，识别市场中的异常行为，如欺诈检测、价格异常波动等。

品牌形象研究

分析消费者对不同品牌的认知和感受，以确定品牌在市场中的位置和形象。