CxHub客户体验社区-用户研究、体验爱好者学习交流社区，专注客户体验(CX)研究。
社交媒体
从两个角度进行理解：
①它是一个效率管理模型
IPA（Important-Performance Analysis）分析模型是由Martilla J.A. 和 James J.C. 在1977 最早提出的，起先用于汽车产品属性分析，目的是为了可以深入了解公司在营销组合的哪一方面应该给予更多的关注，并识别可能消耗太多资源的领域。
②它是一个体验管理模型
因模型本身足够直观、易用性强，被商业和学界广泛应用在用户体验领域。
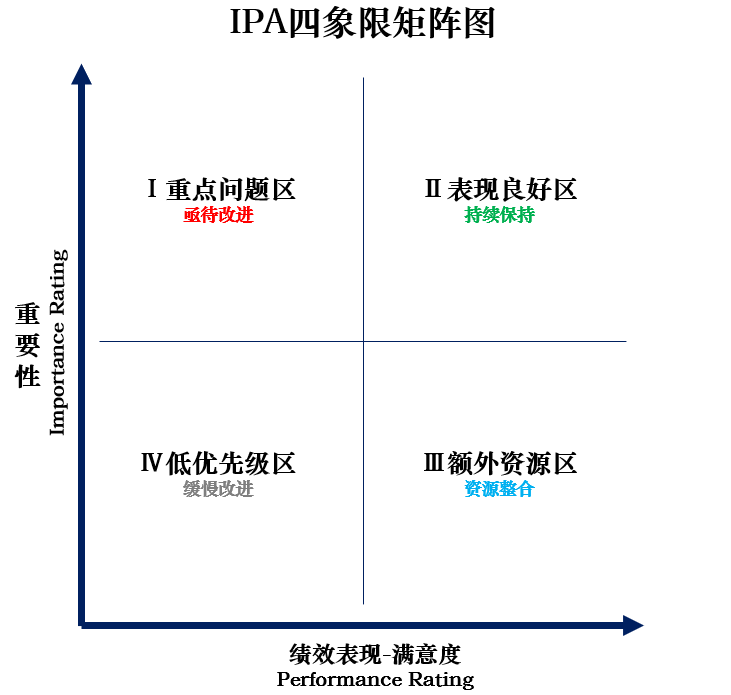
IPA分析法要求受访者对指定调查对象的各项指标从重要性和满意度两个方面来评价。
所以它又被称为“重要性—满意度分析法”。
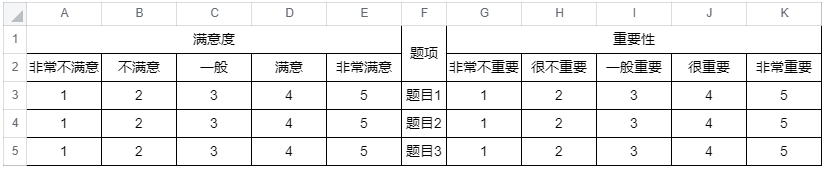
①通过EXCEL & SPSS等数据分析工具，对问卷数据进行录入；
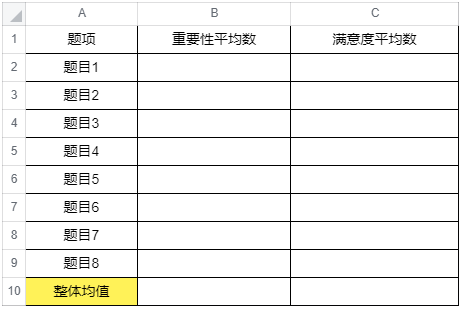
②计算所有题项的平均数（average）并录入到EXCEL & SPSS中；
③绘制散点图，让各指标（题目）自然散落到散点图中；（具体绘制方法可自行网上查阅）
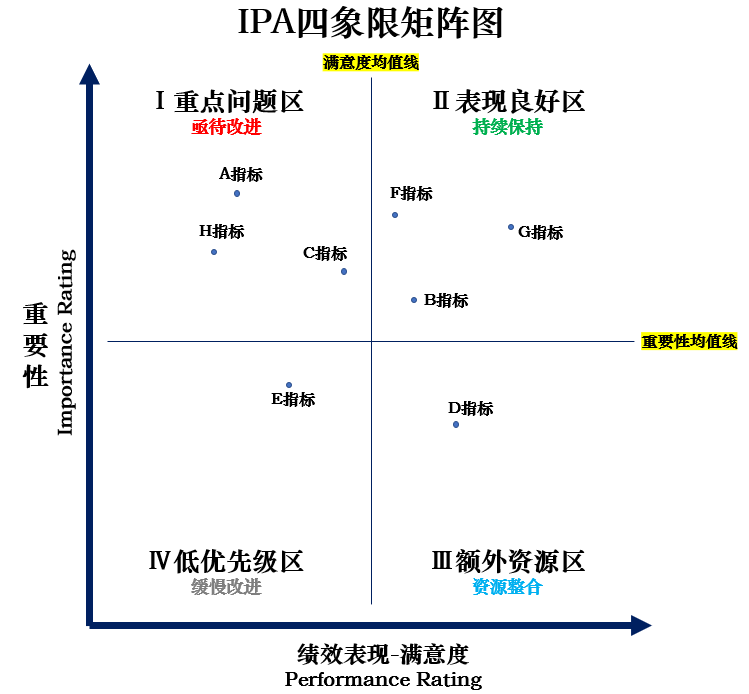
通过以上分析，可清楚地呈现各指标的相对位置，找到后续产品/服务的改善抓手。
①它是主观评价：IPA分析模型是顾客的自述式主观感受在两个维度的投射；
②它是问卷调研：一般以问卷投放的方式实现数据收集；
务必记得这两个特征，与下文内容有紧密关联。
①指标的重要性与满意度两个维度上的变量相互独立；
②指标的满意度与总体满意度评价分别呈线性相关（具有对称性）；
但是在现实调查中，这两个假设几乎难以实现。
①不独立：重要性的评价不可避免地受客户满意度评价的影响。
受访者的评价一般为主观感受，其重要性评价和满意度评价 很难成为互相独立 的变量。比如“我对这个指标的表现越是不满，在重要性打分时倾向给出更高的得分”
②非线性：不同要素的满意度与总体满意度之间会存在非线性相关的可能。
马茨洛和舒华温（Matzler&Sauerwein）发现采用自述方式时，客户对组织满意度评价与重要性感知呈现负相关，即满意度越高，重要性越低。
桑普森和舒华特（Sampson&Showaher）研究发现，组织的满意度增加时，客户的重要性感知与绩效评价间的差距急剧缩小。
日本狩野纪昭教授提出的卡诺（Kano）模型指出，不同要素在消费者的认知中定位是不同的，必备要素满意度低，总体满意度低，而重要性高，当要素满意度高时，总体满意度不一定高（做好这项是必需的）。
③疲劳度：同一问题需做出两次判断（重要性&满意度表现），题量大时，访问时间则成倍增长，答题质量下降。
传统IPA分析法不能满足前提假设，不能真实反映客户实际感知，相应分析结果会产生一定的误导性。
为了保证有效性，有统计学家对传统IPA分析法进行了优化，称为“修正IPA分析法”。
为消除采用自述重要性与满意度的相关性，多数学者建议以引申重要性(implicitly derived importance)来替代自述重要性。
题外话：有一种计算方式是以多元回归方程的系数作为重要性得分。
马茨洛等学者指出，这种方法忽略了满意度要素之间潜在的相关关系，若将其直接代入多元回归模型将会产生严重的多重共线性问题。
邓维兆（deng）提出计算单项满意度与总体满意度之间的偏相关系数来作为引申重要性得分。
偏相关系数排除了其他满意度变量对指定变量与总体满意度之间的相关性影响，只反映该变量与总体满意度之间的净相关。
具体转换方法分为两步：
① 对各要素满意度评价 (A) 取自然对数使之呈现线性分布，计为In (A)；
为什么要呈现线性分布？请看《IPA分析法的前提条件》的部分
② 将In (A)作为自变量，总体满意度作为因变量进行多元回归分析，计算总体满意度与In (A) 之间的偏相关系数Pi，即为引申重要性。
①把满意度指标依次全部取对数。
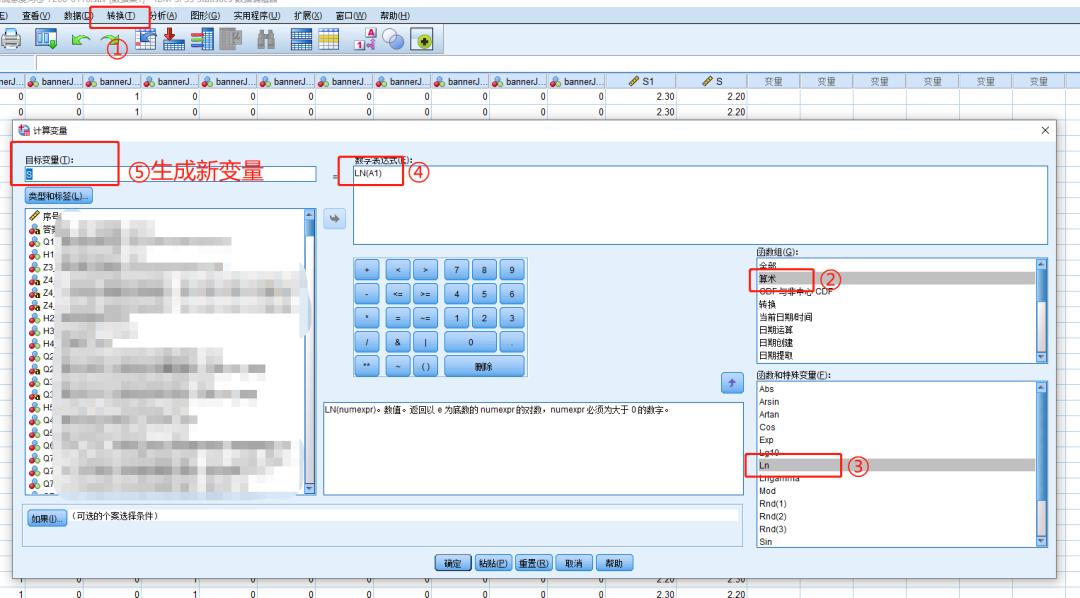
如对SPSS如何实现对数转换不熟悉，可自行网上查阅相关资料，此处不做详细步骤拆解。
②用新增“满意度对数”和“总体满意度”数据进行“偏相关性系数”计算。
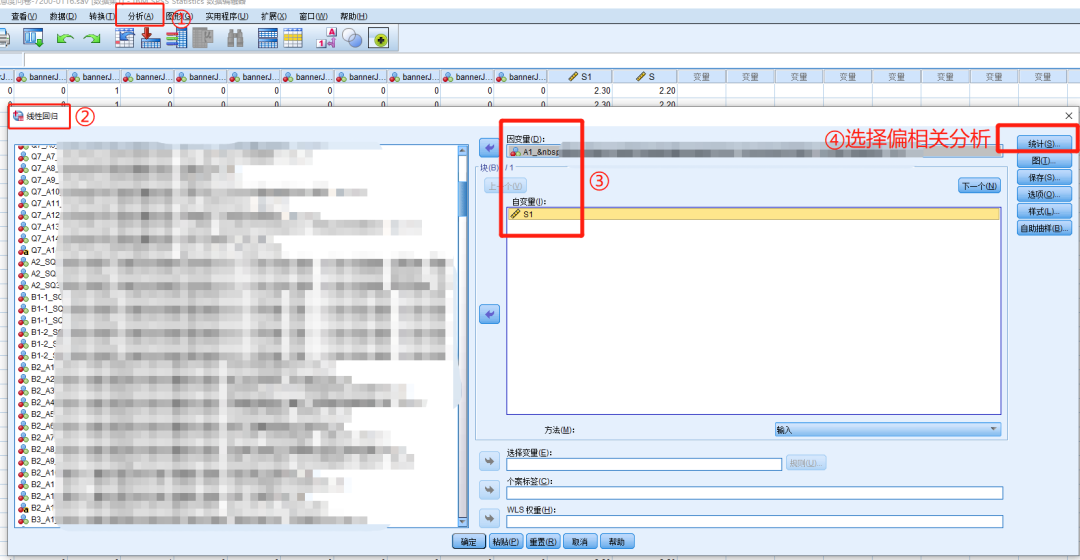
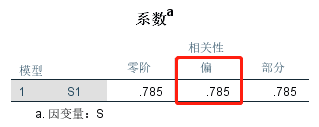
③重复修正IPA操作步骤第二步，获得全部满意度指标的偏相关系数。
为了避免满意度间相关性互相影响，全部指标都要做独立回归，最后在变量视图中备注为“引申重要性”。
④绘制IPA图，Y轴导入新加入的“引申重要性”，代替主观“重要性”。
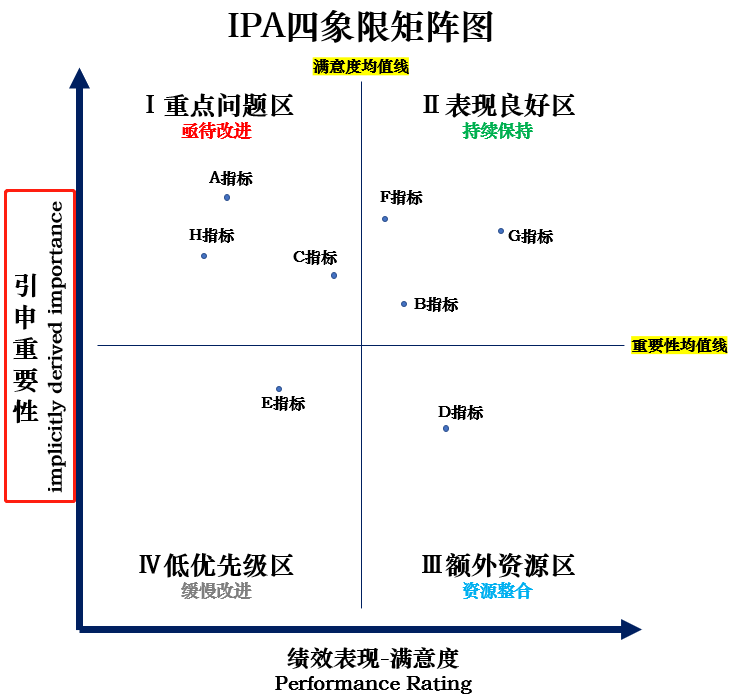
写于最后：鉴于修正IPA分析法对原始IPA分析法的天然优势，笔者建议未来进行相关研究时，可优先考虑此统计方案。
参考文献：
