现如今，「智能驾驶」几乎是汽车行业领军企业着重追求的卖点，它的本质是机器辅助人类驾驶，是涉及到注意力吸引和注意力分散的认知工程学。

「智能驾驶」：自适应巡航控制和转向辅助、车道跟随辅助和防撞辅助等

然而，这些新技术的引入不可避免地增加了人机界面的复杂性，可能对驾驶员产生不利影响。尤其是当驾驶员过度依赖智能驾驶系统时，驾驶表现可能下降，会增加事故风险。

研究表明，驾驶员的注意力分散和疲劳状态通常与心理工作负荷（指驾驶员在驾驶过程中所需处理的信息量）的变化密切相关。

本文将分享一项关于 「高级驾驶辅助系统对驾驶员心理工作负荷的影响」 的研究。

该项研究通过结合ECG、EMG、EDA、EEG（来自 θ 波段的 af4 和 fc6 通道）和眼瞳直径数据，预测心理工作负荷并分为低、适当和高三个级别。

采用 功能线性回归模型 进行分析，发现31种生理变量组合中有9种组合的准确率达到90%。

01 / 实验设置

02 / 结果

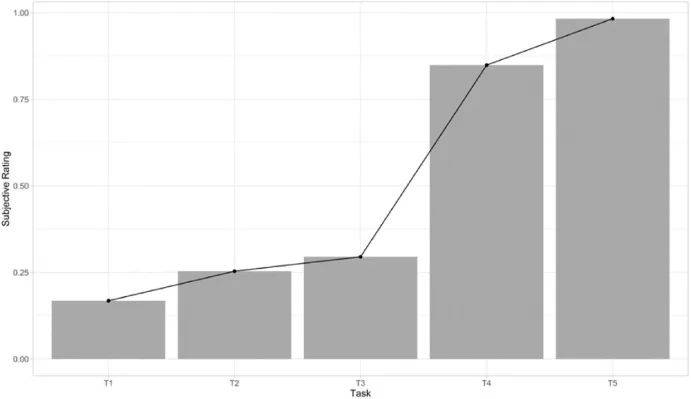
随着实验场景接近尾声，参与者评估他们的心理负荷比场景开始时更高。尤其任务 3[听导航] 和任务 4[发短信] 之间存在显著差距。

在总体预测结果中，功能线性回归模型用于预测心理工作负荷，结果如下：

• 通过比较31个变量组合，平均准确度为0.89，标准差（SD）为0.07。

• 准确度范围相对较窄，位于[0.87, 0.90]之间，标准差范围在[0.05, 0.08]之间。

• 其中，9个变量组合的准确度最高，为0.90，这些组合包括ECG、EDA、EEG（θ波段的af4和fc6），以及ECG、直径和EEG的组合。这些组合的标准差为0.07或0.08。

• 当使用单个信号时，准确度在0.87到0.88之间。例如，使用EDA的准确度为0.87，而使用ECG、EMG、直径和EEG等其他信号时准确度为0.88。

• 使用所有五个信号组合时，准确度最高，达到了0.90。

• 结果表明，随着变量的增加，准确度有所提升。

整体来看，函数线性回归模型在不同信号组合中的表现良好，准确度高且标准差低。结合多种生理信号可以显著提高预测的准确性，证明了使用综合生理信号估计心理工作量的有效性。

表1:分子量预测结果的准确度和标准差

在表2中，函数对函数线性回归模型生成了用于预测心理工作负荷的AUROC（受试者工作特性曲线下面积）值。与表1类似，研究评估了31个不同变量组合的预测性能，结果显示如下：

• 31个组合的平均AUROC值为0.89，标准差为0.08。

• AUROC值的范围较窄，位于0.89到0.90之间，标准差在0.07到0.08之间。

• 值得注意的是，14个组合的AUROC值达到了最高的0.90，其中一些组合包括EDA和EMG，EDA和EEG，ECG、EDA和EEG，以及ECG、直径和EEG的组合。这些组合的标准差为0.07或0.08。

• 当仅使用单个信号时，大多数情况下AUROC值为0.89。例如，仅使用EDA可以获得0.90的AUROC，而使用ECG、EMG、直径和EEG等传感器时AUROC值为0.89。

• 使用所有五个信号时，AUROC值达到最高的0.90。

• 整体来看，纳入更多的生理变量通常会提高AUROC值，增强模型的预测性能。

总的来说，函数对函数线性回归模型在不同变量组合下表现良好，产生高AUROC值且标准差较低。结果表明，结合多个生理信号能够提高预测的准确性，证明了使用综合生理变量来估计心理工作负荷的有效性和优势。

表2:MW预测结果的AUROC值的平均值和标准偏差

该研究提出一种新的分析方法——功能数据分析 (FDA) ，它支持每个单独的数据点都被视为模型的单独输入，将生理数据作为功能对象，允许根据不同参与者的数据生成个性化预测。

FDA能够捕捉数据的复杂关系，并提供更透明的结果解释，相比传统统计方法，FDA能更好地反映心理负荷与生理信号之间的动态关系。

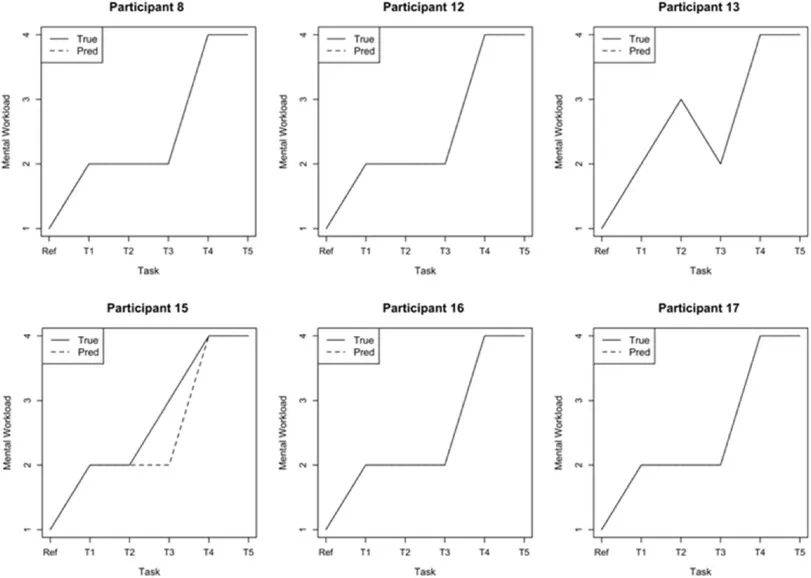
图2展示了参与者之间的心理工作负荷评估差异。不同参与者对任务期间的自我评估有所不同，模型成功捕捉了这些个体差异。模型的优势在于能够准确反映每个参与者的独特心理工作负荷模式。

基于功能数据分析 (FDA) 的方法具有可解释性，而常用的黑盒模型（一种统计模型或机器学习模型）通常无法提供此类信息。黑盒模型在分类心理工作负荷时，难以提取除准确性外的趋势或个性化预测。

本研究利用表现最佳的模型（结合了 EDA、EMG、眼直径和 EEG 的 theta 通道）生成的估计 beta 图，解释了不同信号的总体趋势（如图3所示）。

结果显示，随着参与者面临更复杂的任务，EDA 和眼直径呈现上升趋势，而 EMG 则呈现下降趋势。

此外，生物信号的 beta 图清晰展示了大多数参与者在任务 2 和任务 3 之间心理工作负荷增加的现象，特别是 EMG 和眼直径的显著趋势变化。

03 / 结论

该研究的主要目标是利用 ECG、EMG、EDA、EEG（θ波段的 af4 和 fc6 通道）以及眼径数据来预测驾驶员的心理工作负荷，并将其分为低、中、高三类。

研究基于五种不同的驾驶情境，直接使用原始生理信号作为输入，省略了繁琐的特征工程过程。通过函数线性回归模型进行预测，结果显示在31个变量组合中，9个组合的准确率最高达 0.90 。

相比于其他研究，该研究的准确率虽低于某些特定研究（如Shangguan等人报告的99.5%[1]），但本研究的分类更为细致，涵盖三类心理工作负荷。此外，研究还表明，使用ECG、EEG及另一个信号的组合可以有效预测心理工作负荷。

最后，该研究的创新之处在于不使用特征工程，避免了人为错误和特征相关性的问题，提升了结果的可解释性。 尽管存在参与者性别和年龄不平衡的问题，研究依然达到了0.90的准确率，且性别对生理反应的影响并不显著。 研究结果还强调了利用原始生理信号数据和函数数据分析方法在心理工作负荷预测中的实用性和优势。

（全文结束）

部分素材源于网络

如有侵权，请联系删除